gcd(12,18); ggt(12,18); // (greatest common divisor)
![]()
![]()
Teiler, ggT, kgV, Primzahlen und so weiter
Prof. Dr. Dörte Haftendorn Mathematik mit MuPAD 4.02, (ex. in 3.11 Sept. 05) Feb.07
http://haftendorn.uni-lueneburg.de www.mathematik-verstehen.de
####################################################################
Gliederung:
1. ggt, kgv, Vielfachsummen und erweiterter Euklidischer Algorithmus ##################
2. Primzahlen, Primfaktorzerlegung ##################
3. Teiler, Vielfache ##################
4. Menge Z*(n) der zu n teilerfemden (relativ primen) Zahlen ##################
---------------------------------------eigene Zahlentheorie Ergänzungen---------------------------------------------
delete PACKAGEPATH:endml:=strmatch(NOTEBOOKPATH,"mathe-lehramt", Index)[2]:
gesamtpackpfad:=substring(NOTEBOOKPATH,1..endml+1).pathname("computer","mupad", "packages"):
PACKAGEPATH:=gesamtpackpfad,PACKAGEPATH://Tipps zu Packages siehe unten auf der Seite.
package("zahltheo", Forced):zahltheo::init():export(zahltheo):
---------------------------------------eigene Zahlentheorie Ergänzungen---------------------------------------------
1. ggt, kgv, Vielfachsummen und erweiterter Euklidischer Algorithmus ###
gcd(12,18); ggt(12,18); // (greatest common divisor)
![]()
![]()
lcm(12,18);//kgV(a,b) // (lowest common mnultiple), kgV noch nicht installiert
![]()
hold(gcd(12,18)*lcm(12,18))=hold(12*18);//beispiel für einen allg. Satz.
gcd(12,18)*lcm(12,18) =12*18;
![]()
![]()
In der Kryptographie spielt die Vielfachsummen-Darstellung VSD eine besondere Rolle.
Dabei soll der größte gemeinsame Teiler von a und b als Summe von Vielfachen von a und b geschrieben werden.
ggt(a,b) = s * a + t * b
Man kann die VSD auch als Linearkombination von a und b ansehen.
Man erhält sie mit dem erweiterten Eukidischen Algorithmus:
igcdex(160,111); ggte(160,111) //Erweiterter Euklidischer Algorithmus
![]()
![]()
Die Funktion igcd(a,b) gibt den ggt, s,t als Folge aus,
Die Funktion ggte(a,b) gibt den ggt, s,t als Liste aus,
ggte ist ebenso wie ggt und ggtex in dem eigenen package zahltheo vorhanden.
Es gibt Extraseiten, die die Programmierung genau zeigen.
ggtex(160,111);
160=1*111+49 und es ist VSD 49= 1*160+ (-1)*111
111=2*49+13 und es ist VSD 13= -2*160+ (3)*111
49=3*13+10 und es ist VSD 10= 7*160+ (-10)*111
13=1*10+3 und es ist VSD 3= -9*160+ (13)*111
10=3*3+1 und es ist VSD 1= 34*160+ (-49)*111
ggT(160,111)= 1 VSD 1= 34*160+ (-49)*111
![]()
Probe
34*160 + (-49)*111
![]()
2. Primzahlen, Primfaktorzerlegung ##############################
isprime(100003)
![]()
isprime(100007)
![]()
Primfaktorzerlegung
ifactor(100007)
![]()
ifactor(250348)
![]()
Probe
hold(2^2*7*8941)=2^2*7*8941
![]()
Erzeugung von Primzahllisten
primzahlen:=[]:
if isprime(i)then primzahlen:=primzahlen.[i] end_if $ i=2..700:
pz:=nops(primzahlen);
![]()
matrix([[primzahlen[i*10+k] $ k=1..10] $ i=0..((pz div 10)-1)])

.
primzahlen:=[]:
if isprime(i)then primzahlen:=primzahlen.[i] end_if
$ i=2000..2400:
pz:=nops(primzahlen);
matrix([[primzahlen[i*10+k] $ k=1..10] $ i=0..((pz div 10)-1)])
![]()

numlib::proveprime(37777777777777777777777777777)
![]()
Dies Funktion proveprime arbeitet sicherer als isprime, siehe MuPAD-Hilfe
nextprime(37777777777777777777777777777)
![]()
numlib::prevprime(37777777777777777777777777777)
![]()
numlib::primedivisors(37777777777777777777777777777)
![]()
ifactor(37777777777777777777777777777)
![]()
3. Teiler, Vielfache ####################################
Teilermenge
numlib::divisors(15); teiler(15);
![]()
![]()
Bei der eigenen Prozedur teiler (verwendet auch im TI92/Voyage) kann man die
Teilerpaare sehen.
teiler(24)
![]()
numlib::divisors(24)
![]()
numlib::primedivisors(24)
![]()
Hier sind nur die Primteiler ausgegeben.
so kann man die Exponenten der Primfaktoren sehen.
ifactor(24);
factor(24)
![]()
![]()
Vielfachenfolge
i*7 $ i=1..15
![]()
etwas edler:
[i,i*7] $ i=1..10
![]()
noch edler das Einmaleins
delete a:
matrix([[i*a=i*k $ k=5..10] $i=1..10])
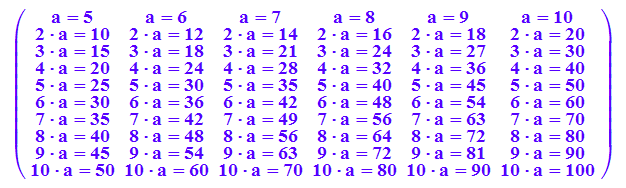
Die Teilerfremden:
Zwei Zahlen a und b heißen teilerfremd, wenn ihr ggt(a,b)=1 ist.
liste:=[]: n:=27:
for i from 1 to n do
if gcd(n,i)=1 then liste:=liste.[i]
end_if:
end_for:
liste
![]()
Diese Befehleszeilen sammeln einfach alle Teilerfremden auf. Sie sind in der Funktion
zstern(n) zusammengefasst, da man diese Menge stets Z*(n) nennt.
zstern(27);
![]()
Die Anzahl der Teilerfremden von n heißt Eulersches Phi(n).
Diese Anzahl erhält man leicht durch die Elemente-Zählfunktion nops(objekt)
oder durch die vorhandene Funktion numlib::phi(n);
numlib::phi(27);
nops(zstern(27));
![]()
![]()
Weiteres: Hilfe, Inhalte, Zahlentheorie
_____________________________________________________________
Tipps zu Packages:
gesamtpackpfad
![]()
Unter Ansicht->Optionen->Kern können Sie in der Zeile Packages diesen String (ohne die "") eintragen,
bzw. den Pfad auf Ihrem Computer,( interaktiv dort das Entsprechende auswählen).
Nach dem erneuten Öffnen von MuPAD behält das
System diesen Pfad und Sie können den obigen winzig gedruckten Teil Auskommentieren /*....*/ deaktivieren.