Dreiblatt
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, Jan. 07 Update 10.01.07
Web: www.mathematik-verstehen.de http://haftendorn.uni-lueneburg.de
Konstruktionsbescheibung für das Dreiblatt
1) Wähle M auf der x-Achse und um M einen Kreis c durch den Urspung B.
sein anderer Schnittpunkt mit der x-Achse sei C.
2) Setze Q frei auf dem Kreis c.
3) Fälle das Lot von Q auf die x-Achse, der Fußpunkt sei D.
4) Spiegele C an D. Es ergibt sich E.
5) A sei Mittelpunkt der Strecke BE.
6) d sei der Kreis um A durch B.
7) Kreis d schneidet die Gerade BQ in P.
8) Gesucht ist der Ort von P, wenn Q auf dem Kreis c läuft.
Anmerkung: die Konstruktion erzwingt, dass die Strecken e und f gleich sind.
----------------------------------------------------------------------------------------------------------
Es ergibt sich die Polargleichung r=r(t):
dreiblattpol:=2*R*(2*cos(t)^2-1)*cos(t);
![]()
R:=1:
dreiblatt:=plot::Polar([dreiblattpol,t],t=0..a,a=0..2*PI,
LineWidth=0.6):
plot(dreiblatt /*,Axes=None*/)
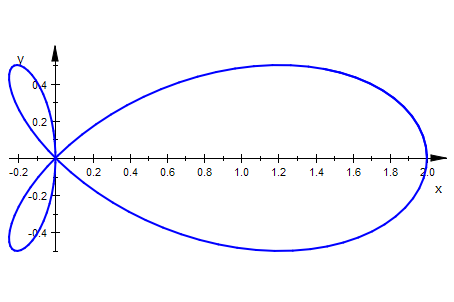
.
Als implizite Gleichung ergibt sich:
dreiblattImp:=(x^2+y^2)^2=2*R*x*(x^2-y^2);
plot(plot::Implicit2d(dreiblattImp,
x=-0.5..2,y=-0.5..0.5, Scaling=Constrained))
![]()
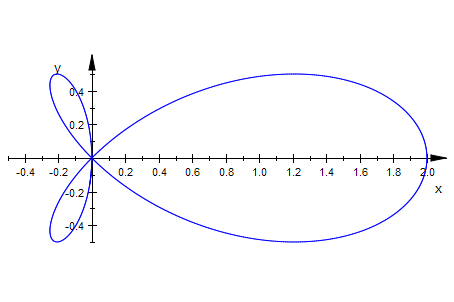
.Das passt.
In Polor-kartesischer Koppelung ergibt sich:
r:=t->2*R*(2*cos(t)^2-1)*cos(t);
archi:=plot::Polar([r(t),t],t=0..ende,ende=0..2*PI,
LineWidth=1, LineColor=RGB::Red, Mesh=400):
archikart:=plot::Curve2d([t,r(t)],t=0..ende,ende=0..2*PI,
LineWidth=1, Mesh=400, LineColor=RGB::Green):
radius:=plot::Line2d([0,0],[r(t)*cos(t),r(t)*sin(t)],t=0..2*PI,LineWidth=0.5):
radiusbetrag:=plot::Line2d([0,0],[abs(r(t))*cos(t),abs(r(t))*sin(t)],
t=0..2*PI,LineWidth=0.5,LineColor=[0,1,0]):
radiusordi:=plot::Line2d([t,0],[t,r(t)],t=0..2*PI,LineWidth=0.5):
plot(archi,radiusbetrag,radius,archikart,radiusordi,
AnimationStyle=BackAndForth):
![]()
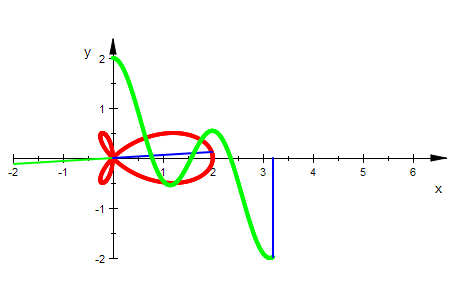
.
Man kann sehr schön sehen, dass dass die keinen Schleifen durch negative Radien entstehen.
Die kartesische r-Funktion aus Bausteinen aufgebaut:
plotfunc2d(2*cos(t)^2-1, (2*cos(t)^2-1)* cos(t),cos(t))
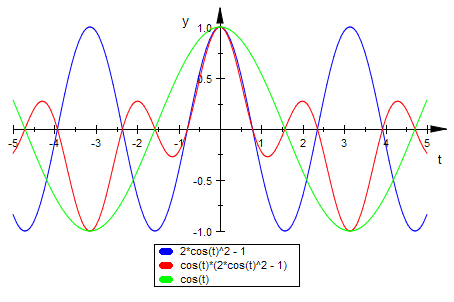
Rot ist r(t) gezeichnet. Ist r(t) punktsymmetrisch zu (PI/2 , 0) ??
r(t);
(2*cos(t)^2-1)* cos(t)
![]()
![]()
.
plotfunc2d(r(PI/2-t),-r(PI/2+t))
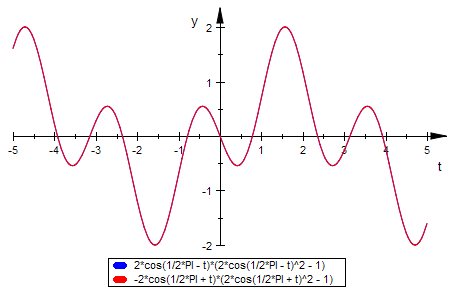
r(PI/2-t);
rr:=t->2*sin(t)*(2*sin(t)^2-1);
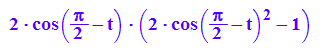
![]()
.
plotfunc2d(rr(t),-rr(-t),r(PI/2-t))
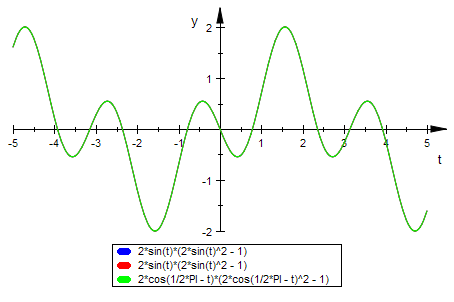
Also sind die beiden Zipfel des Dreiblattes kongruent.
Wo sind Nullstelle der r-Funktion?
r(t)
![]()
Natürlich bei allen cos-Nullstellen und dann noch bei den Nullstellen der Klammer:
solve(2*cos(t)^2-1=0,t)
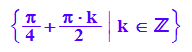
In der Konstruktion ist das der Fall, wenn Q über M liegt. Dann ist nämlich D=M und
A=B=Urspung, damit liegt auch P im Urspung.