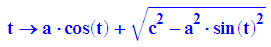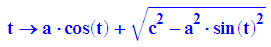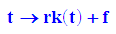Kreis-Konchoiden, c<a
=Kreissehnenkurven
Anregung zu ausführlicherer Untersuchung von Zvonimir Durcevic, Wien
Prof. Dr. Dörte Haftendorn, Mathematik mit Mupad 3 im Juli 05

Polardarstellung von Kreisen um C=(a,0) mit Radius c

• rk:=t->a*cos(t)+sqrt(c^2-a^2*sin(t)^2)

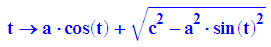
Polardarstellung von Konchoiden zu diesen Kreisen

• r:=t->rk(t)-f

• rr:=t->rk(t)+f

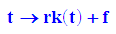
mit +f wäre auch möglich, von Herrn Durcevic nicht gemeint.

• a:=4:c:=3:

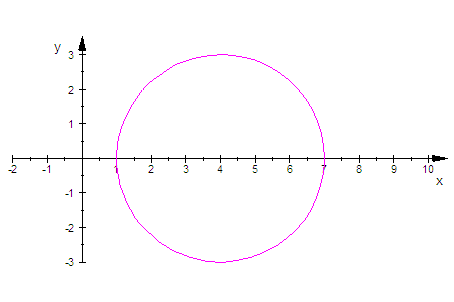
• kreis:=plot::Polar([rk(t),t],t=0..2*PI,LineColor=[1,0,1]
  ,ViewingBox=[-2..10,-c..c]):
  plot(kreis)

• rk(t)

• delete(f):

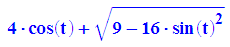
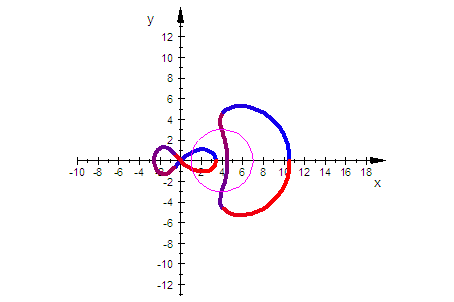
Hier setzen sich die Graphen auf besondere Weise zusammen.
####################################
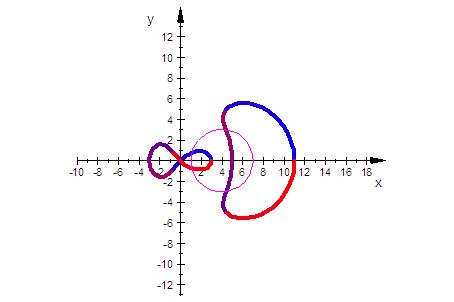
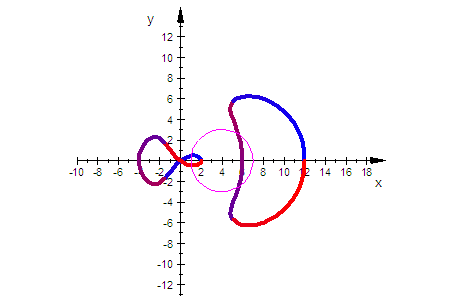
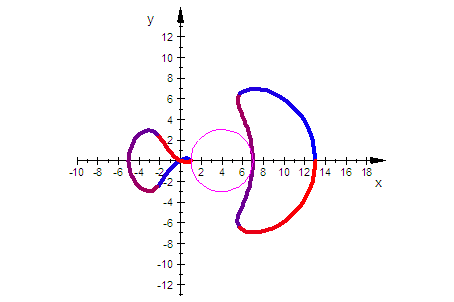
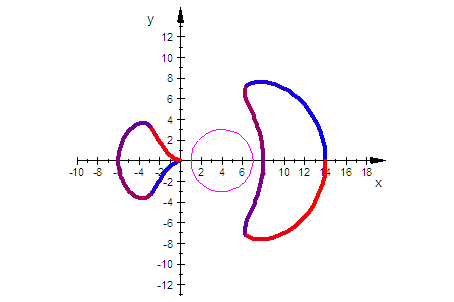
Animation

• plot(plot::Polar([r(t),t],t=0..2*PI,
  LineColorFunction=(t->[t/6,0,1-t/6]),LineWidth=1,f=1..10),
  plot::Polar([rr(t),t],t=0..2*PI,
  LineColorFunction=(t->[t/6,0,1-t/6]),LineWidth=1,f=1..10),
  kreis,ViewingBox=[-10..18,-13..13]
  )

• plot(plot::Polar([r(t),t],t=0..2*PI,
  LineColorFunction=(t->[t/6,0,1-t/6]),LineWidth=1),
  plot::Polar([rr(t),t],t=0..2*PI,
  LineColorFunction=(t->[t/6,0,1-t/6]),LineWidth=1),
  kreis,ViewingBox=[-10..18,-13..13]
  )$ f=1..10