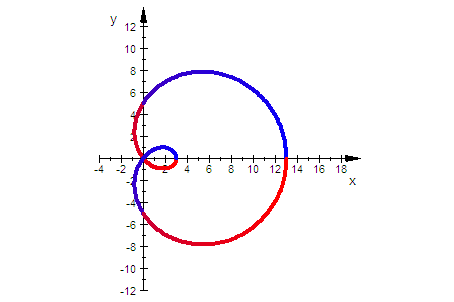
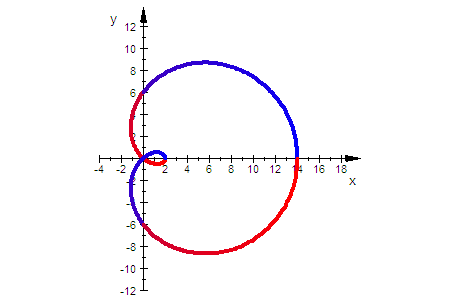
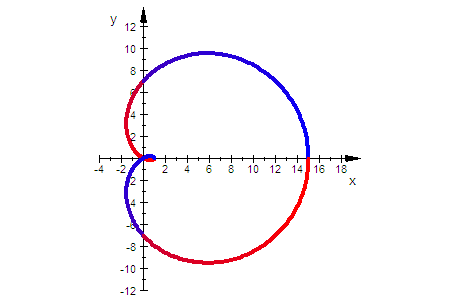
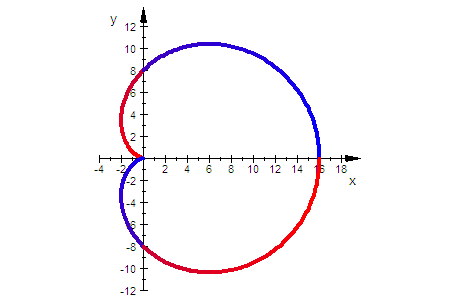
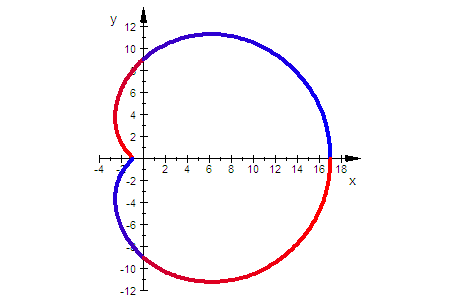
Kreis-Konchoiden, c=a Pascalsche Schnecken
=Kreissehnenkurven
Anregung zu ausfühlicherer Untersuchung von Zvonimir Durcevic, Wien
Prof. Dr. Dörte Haftendorn, Mathematik mit Mupad 3 im Juli 05

Polardarstellung von Kreisen um C=(a,0) mit Radius c

• rk:=t->a*cos(t)+sqrt(c^2-a^2*sin(t)^2)

Polardarstellung von Konchoiden zu diesen Kreisen

• r:=t->rk(t)-f

• rr:=t->rk(t)+f

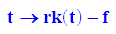
mit +f wäre auch möglich, von Herrn Durcevic nicht gemeint.

• a:=4:c:=4:

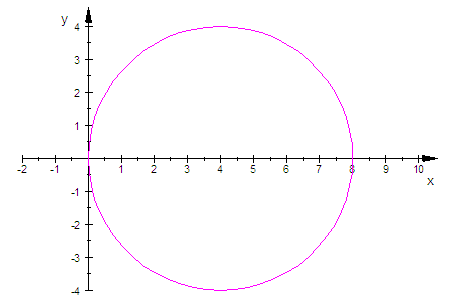
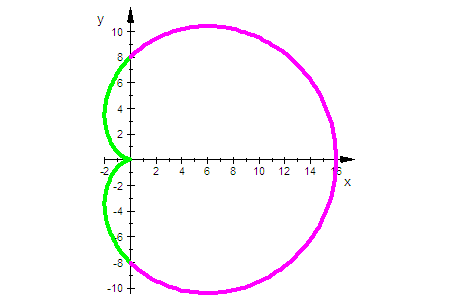
• kreis:=plot::Polar([rk(t),t],t=0..2*PI,LineColor=[1,0,1]
  ,ViewingBox=[-2..10,-c..c]):
  plot(kreis)

• rk(t)

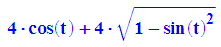
• f:=8:
  konch:=plot::Polar([r(t),t],t=-PI/2..1*PI/2,
  Color=[0,1,0],LineWidth=1):
  konch2:=plot::Polar([rr(t),t],t=-PI/2..1*PI/2,
  Color=[1,0,1],LineWidth=1):
  plot(konch,konch2)

• delete(f):

• allef:=(plot::Polar([r(t),t],t=3*PI/2..4*PI/2,LineWidth=1,
  LineColorFunction=(t->[t/6,0,1-t/6]))$f=1..5):
  allef2:=(plot::Polar([r(t),t],t=0..PI/2,LineWidth=1,
  LineColorFunction=(t->[t/6,0,1-t/6]))$f=1..5):
  allef3:=(plot::Polar([rr(t),t],t=0..PI/2,LineWidth=1,
  LineColorFunction=(t->[t/6,0,1-t/6]))$f=1..5):
  allef4:=(plot::Polar([rr(t),t],t=3*PI/2..4*PI/2,LineWidth=1,
  LineColorFunction=(t->[t/6,0,1-t/6]))$f=1..5):

• plot(allef,allef2,allef3,allef4,kreis)

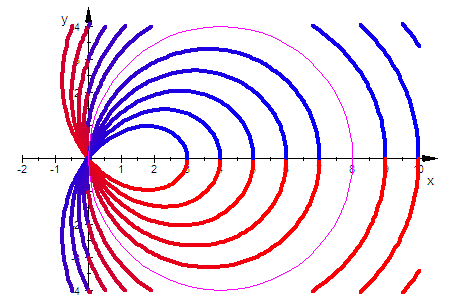
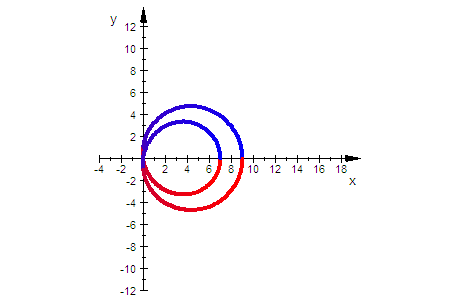
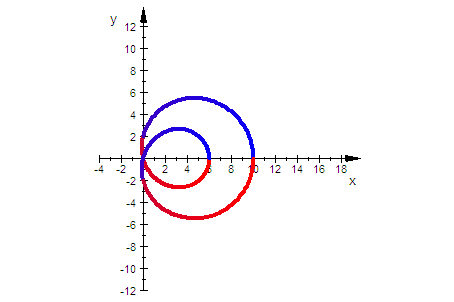
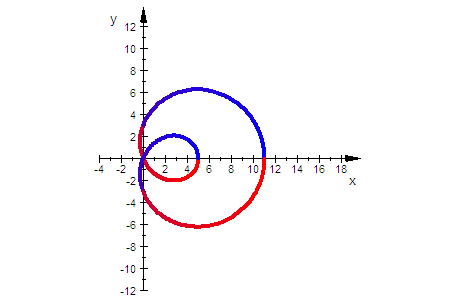
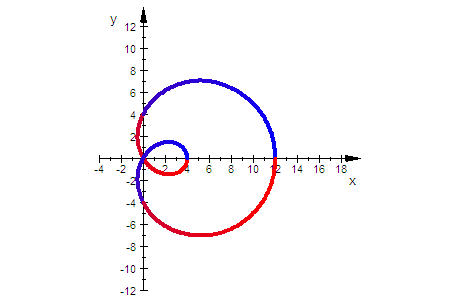
f=1 ist die äußere Kurve, es folgen 2,3,4
rechter Kurvenpunkt ist a+c-f
t=0 ist blau, t= Pi ist lila, t=2Pi ist rot
rechter Schlaufenpunkt ist bei a-c+f

• allef:=(plot::Polar([r(t),t],t=3*PI/2..4*PI/2,LineWidth=1,
  LineColorFunction=(t->[t/6,0,1-t/6]))$f=6..9):
  allef2:=(plot::Polar([r(t),t],t=0..PI/2,LineWidth=1,
  LineColorFunction=(t->[t/6,0,1-t/6]))$f=6..9):
  allef3:=(plot::Polar([rr(t),t],t=0..PI/2,LineWidth=1,
  LineColorFunction=(t->[t/6,0,1-t/6]))$f=6..9):
  allef4:=(plot::Polar([rr(t),t],t=3*PI/2..4*PI/2,LineWidth=1,
  LineColorFunction=(t->[t/6,0,1-t/6]))$f=6..9):
  plot(allef,allef2,allef3,allef4,kreis,
  ViewingBox=[-4..18,-12..12])
  

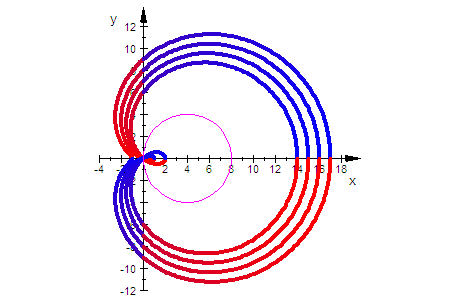
Diese besondere Lage entsteht bei c=f
####################################
Animation , in dieser Art merkwürdige Äste, besser unten

• plot(plot::Polar([r(t),t],t=0..2*PI,
  LineColorFunction=(t->[t/6,0,1-t/6]),LineWidth=1,f=1..12),
  plot::Polar([rr(t),t],t=0..2*PI,
  LineColorFunction=(t->[t/6,0,1-t/6]),LineWidth=1,f=1..12),kreis)

• plot(
  plot::Polar([r(t),t],t=3*PI/2..4*PI/2,LineWidth=1,
  LineColorFunction=(t->[t/6,0,1-t/6]),f=1..9),
  plot::Polar([r(t),t],t=0..PI/2,LineWidth=1,
  LineColorFunction=(t->[t/6,0,1-t/6]),f=1..9),
  plot::Polar([r(t),t],t=0..PI/2,LineWidth=1,
  LineColorFunction=(t->[t/6,0,1-t/6]),f=1..9),
  plot::Polar([rr(t),t],t=0..PI/2,LineWidth=1,
  LineColorFunction=(t->[t/6,0,1-t/6]),f=1..9),
  plot::Polar([rr(t),t],t=3*PI/2..4*PI/2,LineWidth=1,
  LineColorFunction=(t->[t/6,0,1-t/6]),f=1..9),
  ViewingBox=[-4..18,-12..12])
  

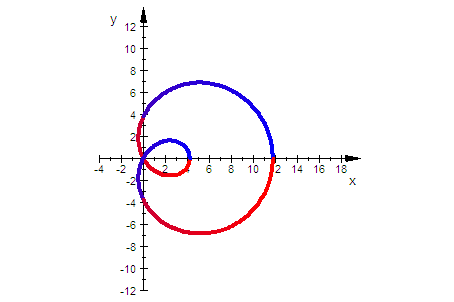
• plot(
  plot::Polar([r(t),t],t=3*PI/2..4*PI/2,LineWidth=1,
  LineColorFunction=(t->[t/6,0,1-t/6])),
  plot::Polar([r(t),t],t=0..PI/2,LineWidth=1,
  LineColorFunction=(t->[t/6,0,1-t/6])),
  plot::Polar([r(t),t],t=0..PI/2,LineWidth=1,
  LineColorFunction=(t->[t/6,0,1-t/6])),
  plot::Polar([rr(t),t],t=0..PI/2,LineWidth=1,
  LineColorFunction=(t->[t/6,0,1-t/6])),
  plot::Polar([rr(t),t],t=3*PI/2..4*PI/2,LineWidth=1,
  LineColorFunction=(t->[t/6,0,1-t/6])),
  ViewingBox=[-4..18,-12..12])$f=1..9