hunde:=(x^2+y^2)*(4-x)^2=64*x^2
![]()
Strophoide und Hundekurve
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, Jan. 07 Update 10.01.07
Web: www.mathematik-verstehen.de http://haftendorn.uni-lueneburg.de
#######################################################################
Sowohl manche Hundekurven als auch die Strophoide sehen schlaufenförmig aus.
Man kann nun untersuchen, ob die Strophoide eine spezielle Hundekurve ist.
hunde:=(x^2+y^2)*(4-x)^2=64*x^2
![]()
Dabei kommt nur eine Hundekurve infrage, bei der Leine doppelt so lang ist wie die
Entfernung a des Baumes von der Straße. Hier ist a= 4 gesetzt.
Das schränkt die Allgemeinheit nicht ein, da alle Strophoiden durch zentrische Streckung
auseinander hervorgehen. ( siehe Polargleichung)
stropho:=(x-4)^2*(x^2+y^2)=4^2*y^2
![]()
Beide Gleichungen ähneln sich in verblüffender Weise.
hundeg:=plot::Implicit2d(hunde,x=-4..8,y=-4..4):
strophog:=plot::Implicit2d(stropho,x=-4..8,y=-4..4,
LineColor=[1,0,0]):
asyh:=plot::Line2d([4,-4],[4,4]):
asys:=plot::Line2d([8,-4],[8,4], LineWidth=2,
LineStyle=Dashed,LineColor=[1,0,1]):
plot(hundeg,asyh,asys, strophog);
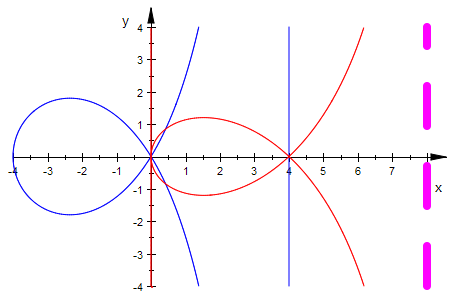
Mindestens muss man die blaue Hundekurve um 4 Einheiten nach rechts schieben.
Vielleicht erreicht man dann noch etwas mit Stauchen.
verHunde:=((x^2+y^2)*(4-x)^2=64*x^2)|x=x-a;
verHundeg:=plot::Implicit2d(verHunde|a=4,x=-4..8,y=-4..4):
linie:=plot::Line2d([5.334,0],[5.334,4]):
linies:=plot::Line2d([5.36,0],[5.36,2],
LineStyle=Dashed,LineColor=[1,0,1]):
asy:=plot::Line2d([8,-4],[8,4]):
asys:=plot::Line2d([8,-4],[8,4], LineWidth=1,
LineStyle=Dashed,LineColor=[1,0,1]):
plot(verHundeg,asy,asys,strophog,linie, linies):
![]()
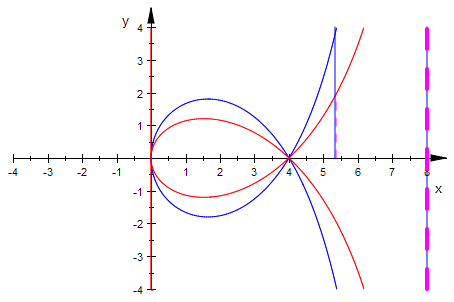
Nun liegen alle wesentlichen Elemente aufeinander. An den Ordinaten bei 5
ist zu sehen, dass ein Stauchfaktor etwa 2 sein müsste. Das ist aber für die
Schlaufen zuviel. Daher kann die Strophoide nicht durch durch eine Hundekurve dargestellt
werden.
Im Übrigen hat die Hundekurve noch einen weiteren Ast, der mit der Strophoide nichts zu tun hat.
Dafür hat diese Stophoidengleichung überflüssigerweise noch die y-Achse als Lösung.
Dieses Beispiel zeigt auch, dass man die algebraischen Kurven nicht grob vom Aussehen her
richtig bestimmen kann.