plot(keg, eb,waag,ko,nv, Scaling=Constrained, Axes=None)

Dandelinsche Kugel im Kegel, Parabel
Prof. Dr. Dörte Haftendorn Nov. 06, http://haftendorn.uni-lueneburg.de
-------------------------------------------------------------------------------------------------------------------------------------
Die Schnittkurve eines Kegels und einer Ebene parallel zur Mantellinie
ist eine Parabel. Beweis unten
alpha:=PI/6:betta:=PI/6: m:=3:xmin:=-11:xmax:=11: R:=xmax:
keg:=plot::Surface([h*tan(alpha)*cos(t),h*tan(alpha)*sin(t),-h],
t=0..2*PI,h=0..R
,Color=[1,0,0,0.5],FillColorType=Flat, Mesh=[30,30]):
eb:=plot::Implicit3d(-cos(betta)*x+sin(betta)*z=-m*(sin(alpha)+sin(betta)),
x=-R..R,y=-6..6,z=-R..0,
FillColorType=Flat,FillColor=[1,0.5,0,1]):
waag:=plot::Function3d(-m*cos(alpha)*cos(alpha),
x=-6..6,y=-6..6,
FillColorType=Flat,FillColor=[0,0.5,0,1]):
ko:=plot::Sphere(m*sin(alpha),[0,0,-m]):
nv:=plot::Arrow3d([-5*cos(betta),0,5*sin(betta)]):
plot(keg, eb,waag,ko,nv, Scaling=Constrained, Axes=None)

uf1:=m*sin(alpha)*cos(betta):
vf1 :=m*(1+sin(alpha)*sin(betta)) :
F1:=[uf1,0,-vf1]:
Brennpunkt
F1g:=plot::Point3d(F1, PointSize=40,
PointColor=RGB::Black):
Wo liegen die Schnittpunkte von Kegel und Ebene?
hw:=m*cos(alpha)^2:
hh:=2*m/(cos(t)+1):ta:=-2:ti:=2:
P:=[(hh*tan(alpha))*cos(t),hh*tan(alpha)*sin(t),-hh]:
P0:=[hh*tan(alpha)*cos(t),0,-hh]:
H0:=[(2*m*tan(alpha)-uf1),0,-hw]:
H:=[(2*m*tan(alpha)-uf1),hh*tan(alpha)*sin(t),-hw]:
A:=[-uf1,0,-hw]:
B:=[-hh*tan(alpha),0,-hh]:
J:=[m*cos(alpha)*sin(alpha)*cos(t),m*cos(alpha)*sin(alpha)*sin(t),-hw]:
Pg:=plot::Point3d(P,t=ti..ta, PointSize=4, PointColor=RGB::Red):
P0g:=plot::Point3d(P0,t=ti..ta, PointSize=4,PointColor=RGB::Red):
Jg:=plot::Point3d(J,t=ti..ta, PointSize=4,PointColor=RGB::Black):
H0g:=plot::Point3d(H0, PointSize=4, PointColor=RGB::Blue):
Hg:=plot::Point3d(H,t=ti..ta, PointSize=4, PointColor=RGB::Blue):
Ag:=plot::Point3d(A, PointSize=4, PointColor=[1,0.5,0]):
Bg:=plot::Point3d(B,t=ti..ta, PointSize=4, PointColor=[0.5,0.5,0]):
lineM1:=plot::Line3d(P,J,
LineWidth=0.8,LineColor=[0,1,0],t=ti..ta):
lineF1:=plot::Line3d(P,F1,
LineWidth=0.8,LineColor=[0,1,0],t=ti..ta):
lineM2:=plot::Line3d(B,A,
LineWidth=0.8,LineColor=[0,1,1],t=ti..ta):
lineP0H0:=plot::Line3d(P0,H0,
LineWidth=0.8,LineColor=[1,0,1],t=ti..ta):
lineH0H:=plot::Line3d(H0,H,
LineWidth=0.8,LineColor=[0,0,0],t=ti..ta):
linePH:=plot::Line3d(P,H,
LineWidth=0.8,LineColor=[1,0,1],t=ti..ta):
kro:=plot::Circle3d(m*cos(alpha)*sin(alpha),
[0,0,-m*cos(alpha)*cos(alpha)],[0,0,1]):
kotr:=plot::Sphere(m*sin(alpha),[0,0,-m],FillColor=[1,0.5,0,0.85]):
kru:=plot::Circle3d(-hh*tan(alpha),[0,0,-hh],t=ti..ta, LineColor=[0,0,1]):
kegleer:=plot::Surface([h*tan(alpha)*cos(t),h*tan(alpha)*sin(t),-h],
t=0..2*PI,h=0..R,Color=[1,0,0,0.25],FillColorType=Flat, Mesh=[30,30]):
plot(eb,kegleer,kotr,kro,waag,F1g,Pg,P0g,Hg,H0g,Ag,Bg,Jg,
lineM1,lineF1,lineM2,lineP0H0,lineH0H,linePH,kru,
Scaling=Constrained, Axes=None):
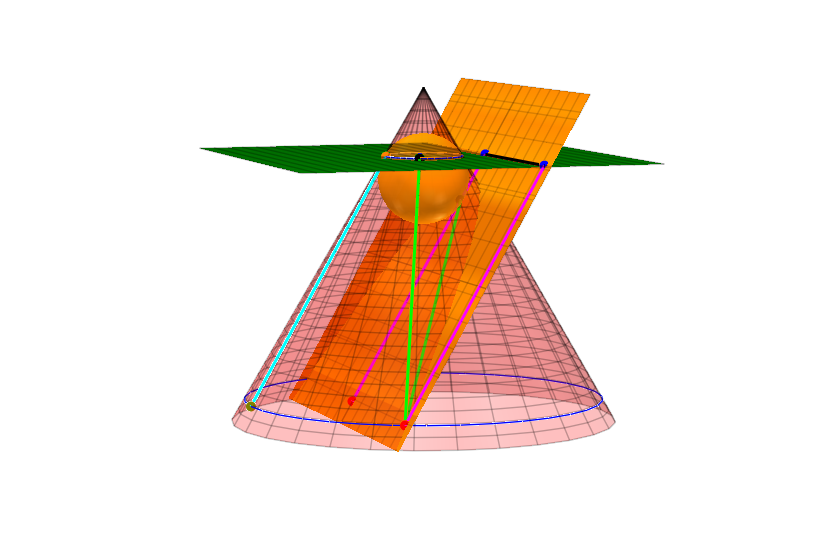
Beweis: Die grüne Ebene ist die Berührebene. Sie schneidet die Schittebene E in der Leitgeraden.
Sie zeigt die y-Richtung an. Auf der Parabel liegt P. Der Punkt, in dem die Kugel E berührt,
ist der Brennpunkt F, PF rechte grüne Strecke. Länge PF= Länge PJ , wobei J am oberen Ende der grünen Mantellinie ist. AB ist die zugehörige hellblaue Mantellinie in der x-z-Ebene. Länge PJ=Länge AB.
Auf E in der x-Z-Ebene verläuft PoHo (lila, hinten) und genau so lang wie AB, es handelt sich um ein Parallelogramm in der x-z-Ebene. PoHo ist nun wieder genauso lang wie PH, es handelt sich um ein Rechteck in der Ebene E. Zusammen gilt in der Schnittebene E, dass P von F denselbene Abstand hat wie von der Leitgeaden, Fußpunkt des Lotes auf die Leitgerade ist H.
Also ist die Schnittkurve eines Kegels und einer Ebene parallel zur Mantellinie eine Parabel. q.e.d.
.