delete r,d:
solve({u^2+v^2=d^2-r^2, u^2+(d-v)^2=r^2},{u,v});
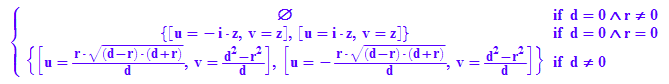
Dandelinsche Kugeln im Zylinder, Ellipsensalami
Prof. Dr. Dörte Haftendorn Nov. 06, http://haftendorn.uni-lueneburg.de
r:=5: d:=8:e:=sqrt(d^2-r^2):
zyl:=plot::Surface([r*cos(t),r*sin(t),z],t=0..2*PI,z=-d-r..d+r
,Color=[1,0,0,0.25],FillColorType=Flat, Mesh=[50,50]):
eb:=plot::Implicit3d(-e*x+r*z=0, x=-r..r,y=-r..r,z=-d-r..d+r):
ko:=plot::Sphere(r,[0,0,d]):ku:=plot::Sphere(r,[0,0,-d]):
nv:=plot::Arrow3d([-e,0,r]):
line:=plot::Line3d([r*cos(t),r*sin(t),d],
[r*cos(t),r*sin(t),-d],
LineWidth=0.8,LineColor=[0,1,0],t=0..2*PI):
delete r,d:
solve({u^2+v^2=d^2-r^2, u^2+(d-v)^2=r^2},{u,v});
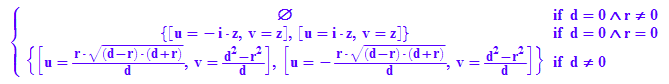
uf := 1/d*r*((d - r)*(d + r))^(1/2):
vf := 1/d*(d^2 - r^2):
r:=5: d:=8:
F1g:=plot::Point3d([uf,0,vf], PointSize=40,
PointColor=RGB::Black):
F2g:=plot::Point3d([-uf,0,-vf], PointSize=40,
PointColor=RGB::Black):
Wo schneidet die grüne Gerade die Ebene?
zz:=e/r*cos(t):
lineM1:=plot::Line3d([r*cos(t),r*sin(t),d],
[r*cos(t),r*sin(t),e*cos(t)],
LineWidth=0.8,LineColor=[0,1,0],t=0..2*PI):
lineM2:=plot::Line3d([r*cos(t),r*sin(t),-d],
[r*cos(t),r*sin(t),e*cos(t)],
LineWidth=0.8,LineColor=[0,1,1],t=0..2*PI):
lineF1:=plot::Line3d([uf,0,vf],
[r*cos(t),r*sin(t),e*cos(t)],
LineWidth=0.8,LineColor=[0,1,0],t=0..2*PI):
lineF2:=plot::Line3d([-uf,0,-vf],
[r*cos(t),r*sin(t),e*cos(t)],
LineWidth=0.8,LineColor=[0,1,1],t=0..2*PI):
kro:=plot::Circle3d(r,[0,0,d],[0,0,1]):
kru:=plot::Circle3d(r,[0,0,-d],[0,0,1]):
kotr:=plot::Sphere(r,[0,0,d],FillColor=[1,0.5,0,0.85]):
kutr:=plot::Sphere(r,[0,0,-d],Color=[1,0.5,0,0.85]):
zylleer:=plot::Surface([r*cos(t),r*sin(t),z],t=0..2*PI,z=-d-r..d+r
,Color=[1,0,0,0.25],FillColorType=Flat, Mesh=[30,30],
ULinesVisible=FALSE,VLinesVisible=FALSE):
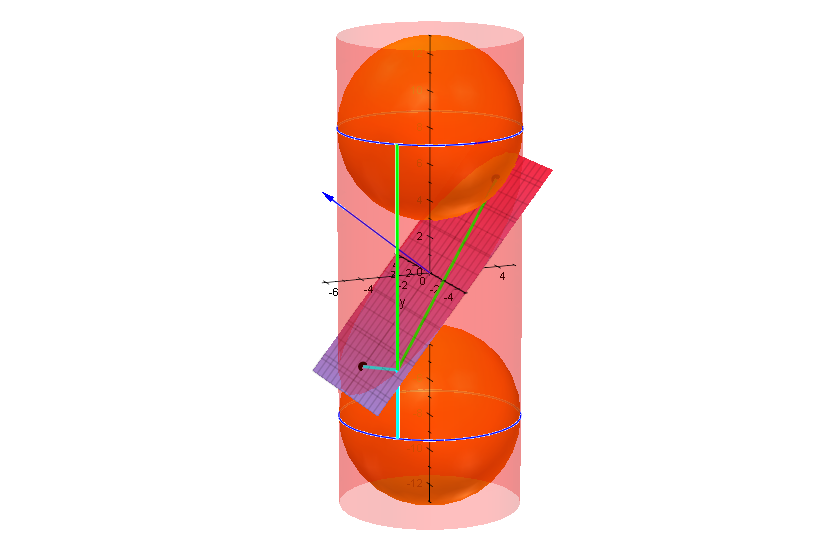
plot(eb,nv,lineM1,lineM2,lineF1,lineF2,F1g,F2g, kro,kru,kutr,
kotr,Axes=Origin,zylleer,
Scaling=Constrained);
.