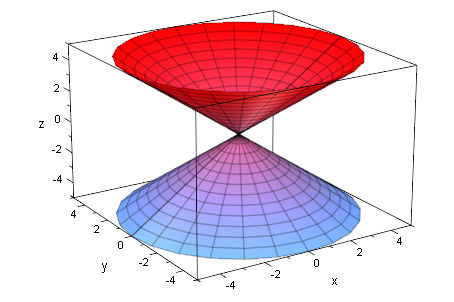
kegDopp:=plot::Surface([r*cos(t),r*sin(t),r],t=0..2*PI,r=-5..5):
plot(kegDopp)
Kegel von Ebenen geschnitten
Prof. Dr. Dörte Haftendorn Feb. 07 MuPAD 4, http://haftendorn.uni-lueneburg.de
#############################################################
Darstellung des Kegels mit Parametern, der Ebenen mit impliziten Gleichungen.
So kann man es auch in Derive 6 machen.
kegDopp:=plot::Surface([r*cos(t),r*sin(t),r],t=0..2*PI,r=-5..5):
plot(kegDopp)

.
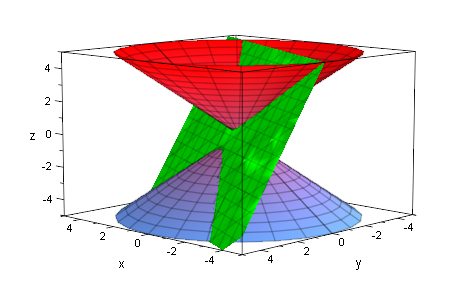
ebh1:=plot::Implicit3d(x+2*y+z=1,x=-5..5,y=-5..5,z=-5..5,
FillColorType=Flat, FillColor=RGB::Green, Mesh=[8,8,8]):
plot(kegDopp,ebh1)
.
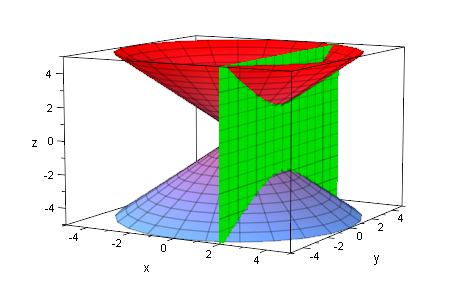
ebh:=plot::Implicit3d(x=2,x=-5..5,y=-5..5,z=-5..5,
FillColorType=Flat, FillColor=RGB::Green, Mesh=[8,8,8]):
plot(kegDopp,ebh)
.
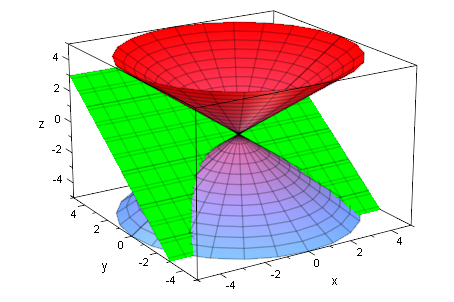
ebp:=plot::Implicit3d(y-z=2,x=-5..5,y=-5..5,z=-5..5,
FillColorType=Flat, FillColor=RGB::Green, Mesh=[8,8,8]):
plot(kegDopp,ebp)
.
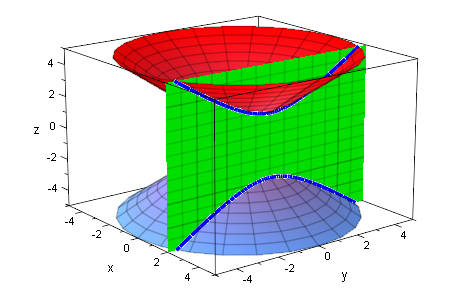
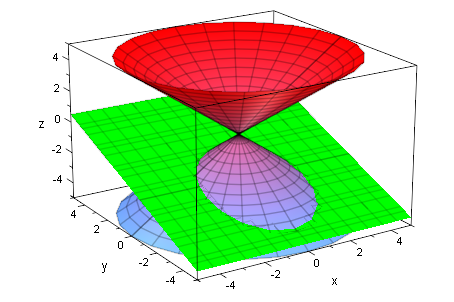
ebe:=plot::Implicit3d(y-2*z=4,x=-5..5,y=-5..5,z=-5..5,
FillColorType=Flat, FillColor=RGB::Green, Mesh=[8,8,8]):
plot(kegDopp,ebe)
Alternative für desselben Kegels implizit,
da werden die Schnitte aber nicht so sauber.
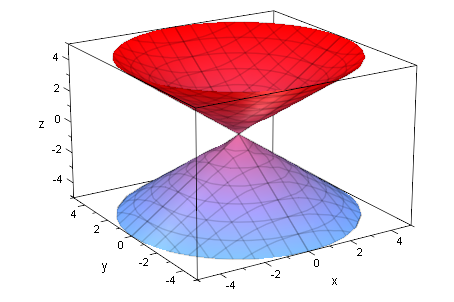
kegDopi:=plot::Implicit3d(x^2+y^2=z^2,x=-5..5,y=-5..5,z=-5..5):
plot(kegDopi)
########################################################
Jetzt sollen die 3d-Kurven dazu dick blau gezeichnet werden.
Sie können von Hand bestimmt werden. Aus dem Gleichungssystem mit der Parameterdarstellung
des Kegels und der Gleichung bder Ebene ist die Parameterdarstellung der Kurve zu gewinnen.
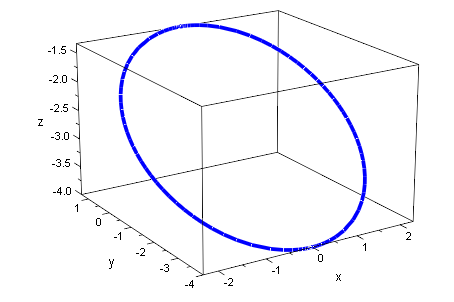
Rechenbeispiel für Ellipse
ell1:=plot::Curve3d([sqrt(-16-16*r-3*r^2),2*r+4,r],
r=-5..5, LineWidth=1):
ell2:=plot::Curve3d([-sqrt(-16-16*r-3*r^2),2*r+4,r],
r=-5..5, LineWidth=1):
plot(ell1,ell2)
plot(kegDopp,ebe,ell1,ell2)
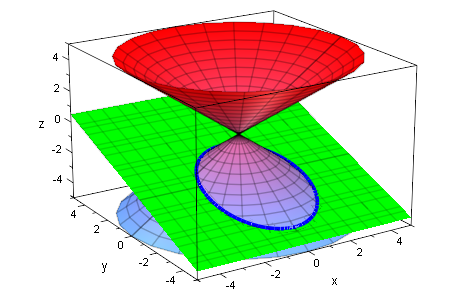
par1:=plot::Curve3d([2*sqrt(-1-r),r+2,r],
r=-5..5, LineWidth=1):
par2:=plot::Curve3d([-2*sqrt(-1-r),r+2,r],
r=-5..5, LineWidth=1):
plot(par1,par2)
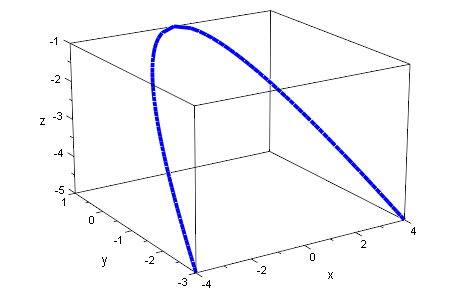
plot(kegDopp,ebp,par1,par2)
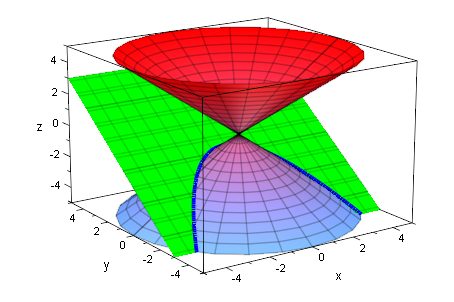
Rechnung mit MuPAD
solve([x=z*cos(t),y=z*sin(t),y=2*z+4],[x,y,z])
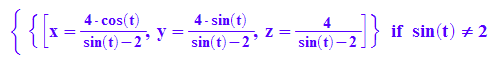
hyp1:=plot::Curve3d([2,2*tan(t),2/cos(t)],
t=-PI..PI, LineWidth=1):
plot(hyp1, ViewingBox=[-5..5,-5..5,-5..5])
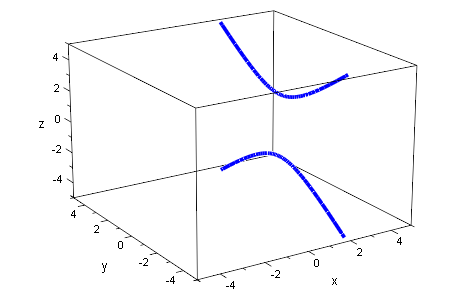
plot(hyp1,ebh,kegDopp, ViewingBox=[-5..5,-5..5,-5..5])