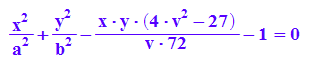ks:=[[a,0],[b,0],[-a,0],[-b,0],[u,v]];
![]()
Kegelschnitt aus 5 Punkten
Prof. Dr. Dörte Haftendorn: Mathematik Nov. 02, mit MuPAD 4, Apr. 08 Update Apr. 08
http://haftendorn.uni-lueneburg.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Eindrucksvoll ist es, in GeoGebra 5 Punkte zu setzen, das Kegelschnitt-Icon zu wählen
und dann an einem der Punkte zu ziehen.
Hier wird dieses rechnerisch nachvollzogen.
Dabei werden 4 der Punkte auf die Achsen gelegt,
damit das Vorgehen einigermaßen übersichtlich bleibt.
Der fünfte Punkt Q(u,v) wird dann erst variiert.
So ist es auch "kegelschnitt-5punkte-reflexion.ggb" gemacht.
ks:=[[a,0],[b,0],[-a,0],[-b,0],[u,v]];
![]()
Allgemeine Quadratische Form, normiert:
qf:=a11*x^2+2*a12*x*y+a22*y^2+a1*x+a2*y-1=0
![]()
qf1:=subs(qf,x=a,y=0);
qf2:=subs(qf,x=0,y=b);
qf3:=subs(qf,x=-a,y=0);
qf4:=subs(qf,x=0,y=-b);
qf5:=subs(qf,x=u,y=v)
![]()
![]()
![]()
![]()
![]()
loe:=op(solve({qf1,qf2,qf3,qf4},{a11,a12,a22,a1,a2}))
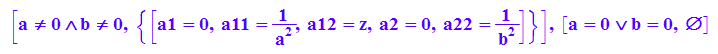
einsetz:=loe[1][2]
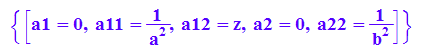
keg:=subs(qf,einsetz[1])
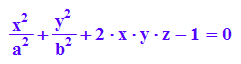
Mit speziellen Werten zum Zeichnen vorbereiten.
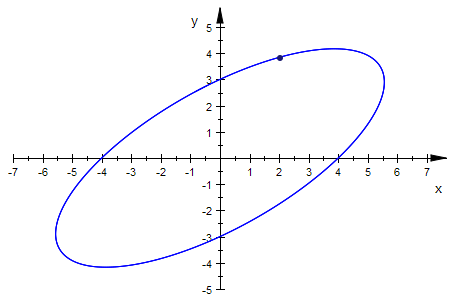
zwert:=solve(keg|[a=4,b=3,x=2,y=7/2],z)[1]
![]()
kege:=subs(keg,z=zwert)
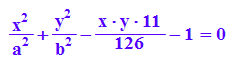
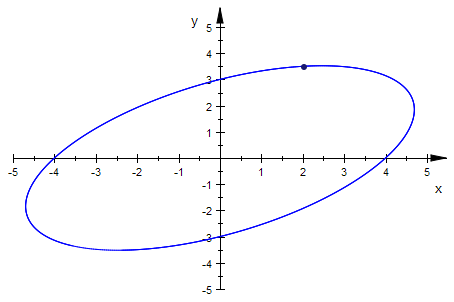
kegeGraph1:=plot::Implicit2d(kege|[a=4,b=3],x=-5..5,y=-5..5):
punkt1:=plot::Point2d([2,7/2]):
plot(kegeGraph1,punkt1)
Nun soll das beweglich gestaltet werden
zwert:=solve(keg|[a=4,b=3,x=2,y=v],z)[1][1]
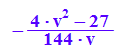
kege:=subs(keg,z=zwert);
punkt:=plot::Point2d([2,v],v=0.1..4):
kegeGraph:=plot::Implicit2d(kege|[a=4,b=3],x=-7..7,y=-5..5,v=0.1..4):
plot(kegeGraph, punkt)