ku1:=plot::Implicit2d(x^2+y^2-25=0,x=-5..5,y=-5..5);
ku2:=plot::Implicit2d(x^2/64+y^2/9-1=0,x=-8..8,y=-5..5, LineColor=[0,1,0]);
kup:=plot::Implicit2d((x^2+y^2-25)*(x^2/64+y^2/9-1)=0,
x=-8..8,y=-5..5, LineColor=[1,0,0]);
![]()
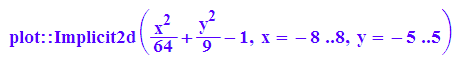
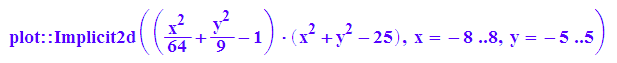
Kreationen mit Produkten algebraischer Kurven
Prof. Dr. Dörte Haftendorn, MuPAD 4, Juni 08 Update 3. Juli 08
Web: http://haftendorn.uni-lueneburg.de www.mathematik-verstehen.de
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Grundidee: Schreibe die Gleichung einer algebraische Kurve als F(x,y)=0,
einer anderen als G(x,y)=0. Dann ist F(x,y)*G(x,y)=0 auch eine algebraische Kurve,
die aus der vereinigten Punktmange beider Kurven entsteht.
3d-Deutung: Wenn man nun aber noch einen Schritt weiter geht und z=P(x,y) schreibt,
dann entsteht eine Raumfläche, deren Schnitt mit der Grundebene (x-y-Ebene) die durch
P(x,y)=0 gegebene Kurve ist.
Wenn man nun noch die Schnitte mit den zur Grundebene parallelen Ebenen betrachtet,
erzeugt man eine beträchtlich erweiterte Kurvenfamilie (siehe ganz unten)
Diese Datei widmet sich allen diesen Gesichtspunkten.
#################################################
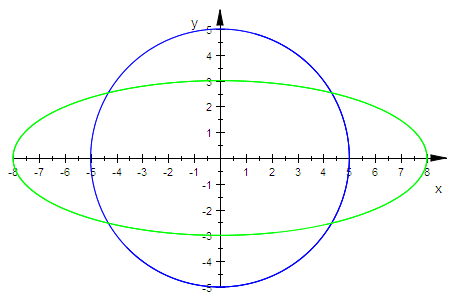
Produkt aus Kreis und Ellipse
ku1:=plot::Implicit2d(x^2+y^2-25=0,x=-5..5,y=-5..5);
ku2:=plot::Implicit2d(x^2/64+y^2/9-1=0,x=-8..8,y=-5..5, LineColor=[0,1,0]);
kup:=plot::Implicit2d((x^2+y^2-25)*(x^2/64+y^2/9-1)=0,
x=-8..8,y=-5..5, LineColor=[1,0,0]);
![]()
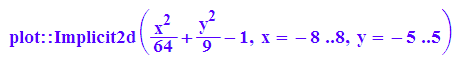
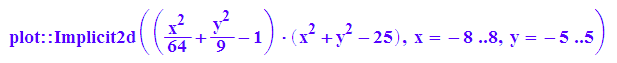
plot(ku1, ku2, Scaling=Constrained);
plot(ku1, ku2,kup, Scaling=Constrained)
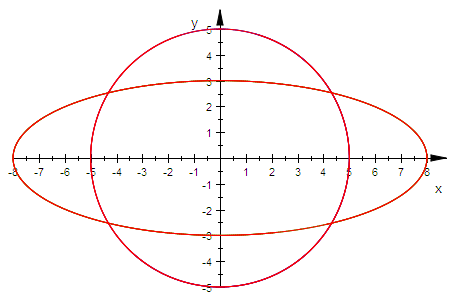
Einstieg in die 3d-Sicht
Elliptisches Paraboloid
z:=(x,y)->x^2/64+y^2/9-1
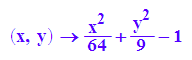
plotfunc3d(z(x,y),a,x=-18..18,y=-12..12,a=-2..4,
LegendVisible=FALSE)
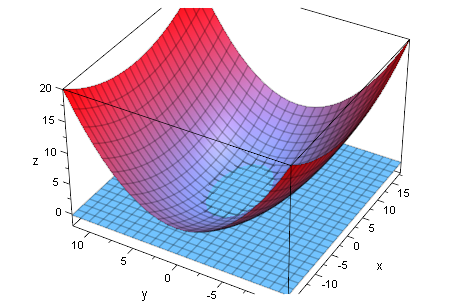

Obiges Produkt mit diversen Schnittebenen
plotfunc3d((x^2+y^2-25)*(x^2/64+y^2/9-1),a,x=-8..8,y=-5..5,
ViewingBoxZRange=-8..30, a=-8..20, LegendVisible=FALSE)
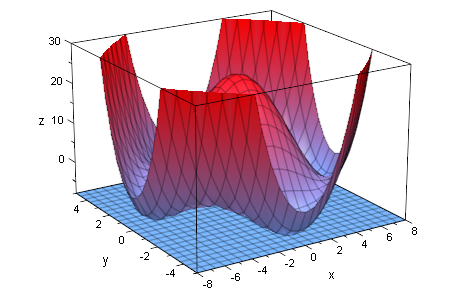

Achtung, 2 Min Rechenzeit, Darstellung un größerem Fenster
plotfunc3d((x^2+y^2-25)*(x^2/64+y^2/9-1),a,x=-10..10,y=-7..7,
ViewingBoxZRange=-8..30, a=-8..20, LegendVisible=FALSE)
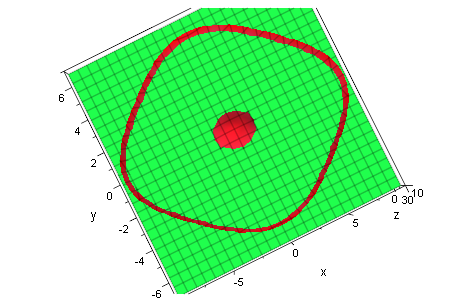

Zurück zur 2d-Sicht
kupro:=plot::Implicit2d((x^2+y^2-25)*(x^2/64+y^2/9-1)=a,x=-8..8,y=-5..5,a=-8..20, LineColor=[0,1,0]);
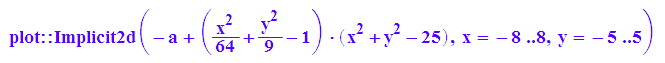
plot(kupro)
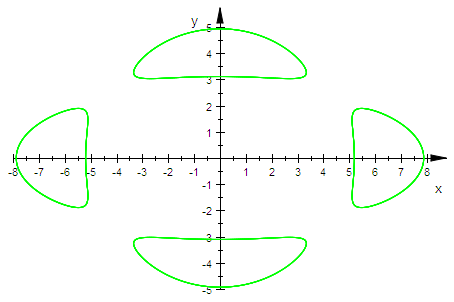

Erkenntnis:
Wenn man diese Kurvenschar hier allein betrachten würde, wären die Erscheinungsformen
vielfältig und unübersichtlich. Betrachtet man aber die 3d-Version, wird alles sofort klar.
Felix Klein hat über diese Schar um 1900(?) eine Abhandlung geschrieben,
heute können das Schüler vollständig erkunden.