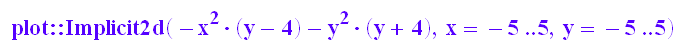algebraischer Kurven 3d
Prof. Dr. Dörte Haftendorn, MuPAD 4, Juni 08 Update 7. Juli 10
Web: http://haftendorn.uni-lueneburg.de www.mathematik-verstehen.de
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Grundidee: Schreibe die Gleichung einer algebraische Kurve als F(x,y)=0,
3d-Deutung: Wenn man nun aber den Schritt in den Raum weiter geht und z=F(x,y) schreibt,
dann entsteht eine Raumfläche, deren Schnitt mit der Grundebene (x-y-Ebene) die durch
F(x,y)=0 gegebene Kurve ist.
Wenn man nun noch die Schnitte mit den zur Grundebene parallelen Ebenen betrachtet,
erzeugt man eine beträchtlich erweiterte Kurvenfamilie (siehe ganz unten)
Diese Datei widmet sich allen diesen Gesichtspunkten.
#################################################
F:=(x,y)->x^2*(4-y)-y^2*(4+y)
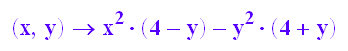
plotfunc3d(F(x,y))
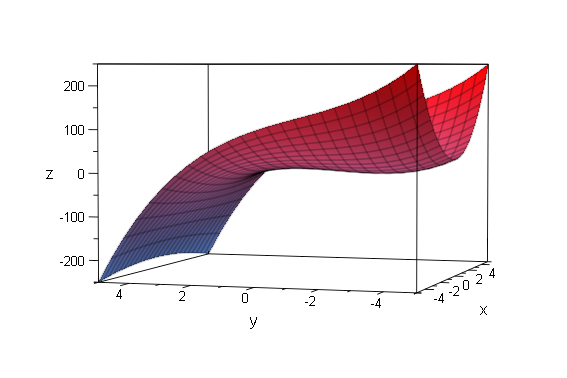
plotfunc3d(F(x,y),ViewingBoxZRange=-10..5)
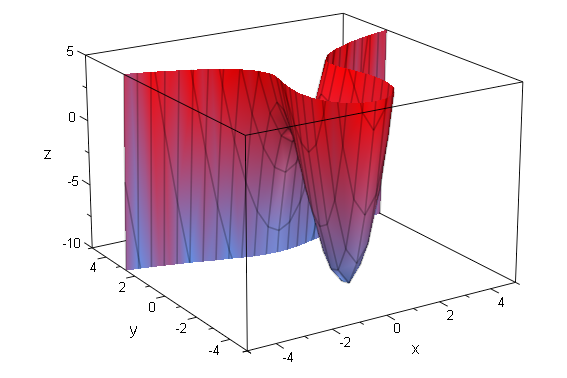
plotfunc3d(F(x,y),Mesh=[50,50],ViewingBoxZRange=-10..5)
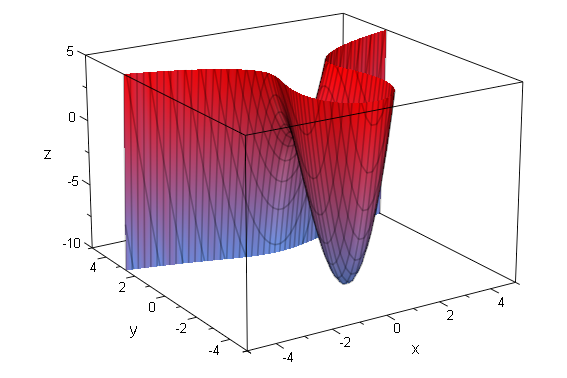
plotfunc3d(F(x,y),0,Mesh=[50,50],ViewingBoxZRange=-10..5)
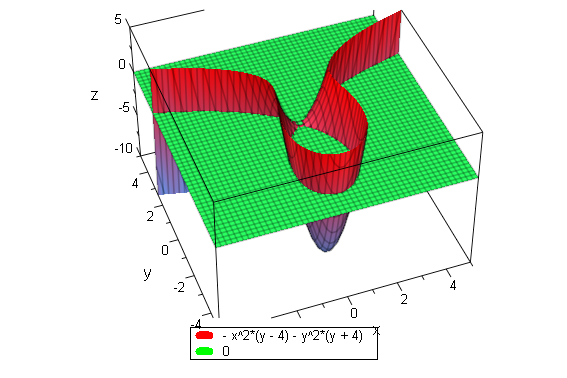
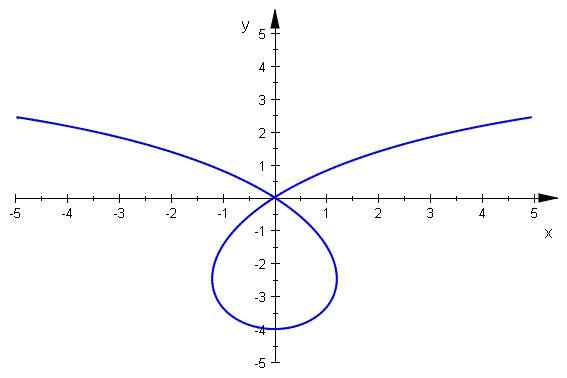
stropho:=plot::Implicit2d(F(x,y)=0,x=-5..5,y=-5..5);
plot(stropho)