par:=x->a*x^2
![]()
Keplersche Regel
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, Update Sept.05
exsistiert auch als MuPAD 3-Version Aug. 05
www.uni-lueneburg.de/mathe-lehramt http:haftendorn.uni-lueneburg.de
---------------------------------------------------------------------------------------------------------
1. Kastengrundlagen rechnen und zeichnen
2. Funktion näherungsweise Integrieren (Aufgabe x+cos(x), Rotation)
3. Für Polynome 3. Grades arbeitet die Kepler-Regel exakt.
#########################################################
delete a,x,ax,r:
1. Kastengrundlagen rechnen und zeichnen
par:=x->a*x^2
![]()
A:=[ax,par(ax)];
B:=[ax-r,par(ax-r)];
Dd:=[ax+r,par(ax+r)];
![]()
![]()
![]()
tangente:=x->(par(ax+r)-par(ax-r))/(2*r)*(x-ax)+par(ax);
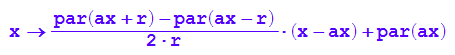
Ee:=[ax-r,tangente(ax-r)];F:=[ax+r,tangente(ax+r)];
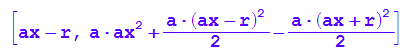
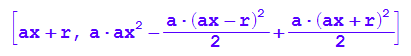
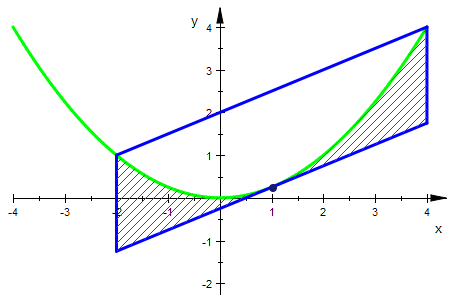
Damit ist der Kasten der Breite 2r an der Stelle ax erzeugt.
a,ax,r;
simplify(int(par(x)-tangente(x), x=ax-r..ax+r))
![]()

kasten:=simplify(2*r*(par(ax-r)-tangente(ax-r)))
![]()
1/3*kasten

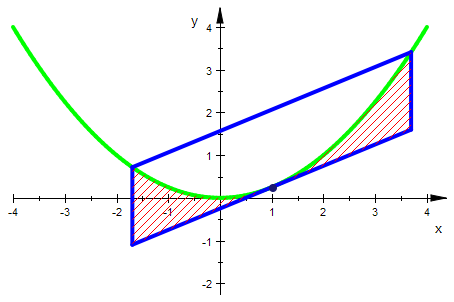
Also nimmt die Parabelfläche 2/3 der Kastenfläche ein
und zwar ist sogar der Wert nicht abhängig von der Stelle sondern
nur von der Parabelöffnung und der Kastenbreite.
####################################################
Zeichnung in Abhängigkeit von r
a:=1/4:ax:=1:
rpolygon:=plot::Polygon2d([Ee,F,Dd,B,Ee],r=0.5..3):
gpar:=plot::Function2d(par(x),x=-4..4, LineColor=RGB::Green):
gA:=plot::Point2d(A, PointSize=2):
gtang:=plot::Function2d(tangente(x),x=-4..4,r=0.5..3):
zwisch:=plot::Hatch(gpar,gtang,ax-r..ax+r,r=0.5..3):
plot(gpar,rpolygon,gA,zwisch, LineWidth=1);

####################################################
Zeichnung in Abhängigkeit von ax
delete ax: r:=3:a:=1/4:
axpolygon:=plot::Polygon2d([Ee,F,Dd,B,Ee],ax=-1..1):
axgA:=plot::Point2d(A, PointSize=2,ax=-1..1):
axgtang:=plot::Function2d(tangente(x),x=-4..4,ax=-1..1):
axzwisch:=plot::Hatch(gpar,axgtang,ax-r..ax+r,ax=-1..1):
plot( gpar,axpolygon,axgA,axzwisch,LineWidth=0.8)

#########################################################
2. Funktion näherungsweise Integrieren
Beispiel: Berechnen Sie das Rotationsvolumen von f um die
x-Achse im Bereich zwischen der Nullstelle und x=3.
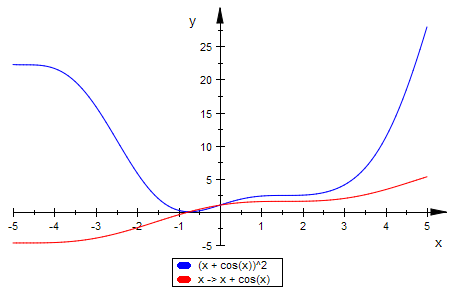
f:=x->x+cos(x)
![]()
fq ist die Funktion, die bei einem Volumenproblem mit f(x)=x+ cos(x) auftritt.
fq:=x->(x+cos(x))^2
![]()
plotfunc2d(fq(x),f)
xs:=numeric::solve(f(x)=0,x)[1];
re:=3.0;
![]()
![]()
plot(plot::XRotate(f(x),x=xs..re))
mi:=(xs+re)/2
![]()
fg:=plot::Function2d(f(x),x=-2..4, LineStyle=Dashed):
fqg:=plot::Function2d(fq(x),x=-2..4, LineColor=[1,0,0]):
ende:=plot::Line2d([re,fq(re)],[re,0]):
mitte:=plot::Line2d([mi,fq(mi)],[mi,0]):
plot(fg,fqg, ende, mitte)
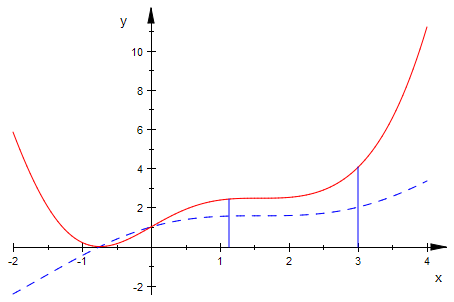
[re-xs, fq(xs),fq(mi),fq(re)];
kl:=[(re-xs)/6, fq(xs),4*fq(mi),fq(re)]
![]()
![]()
Berechnung nach der Kepler-Regel
kepWert:=PI*kl[1]*(kl[2]+kl[3]+kl[4]);
float(kepWert)
![]()
![]()
zum Vergleich mit Integration
PI*int(fq(x),x=xs..re);
float(%)
![]()
![]()
Vergleichszylinder, Radius dem Graphen entnommen
r:=1.6: Vz:=PI*r^2*(3-xs)
![]()
Das passt.
##########################################
Polynome 3. Grades
Ein spezielles Polynom zeigt uns später die allgemein geltenden Eigenschaften.
p3:=x->x^2*(x-4)+10
![]()
delete a,b,c:
x0:=-1:x2:=3: x1:=(x0+x2)/2:
p3(x0),p3(x1),p3(x2)
![]()
Erzeugung der passenden Keplerparabel:
p2:=x->a*x^2+b*x+c:
lo:=solve([p2(x0)=p3(x0),p2(x1)=p3(x1),p2(x2)=p3(x2)],[a,b,c])
![]()
a:=lo[1][1][2]:b:=lo[1][2][2]:c:=lo[1][3][2]:
a,b,c, p2(x)
![]()
plotfunc2d(p2(x),p3(x), ViewingBoxYRange=-5..10)
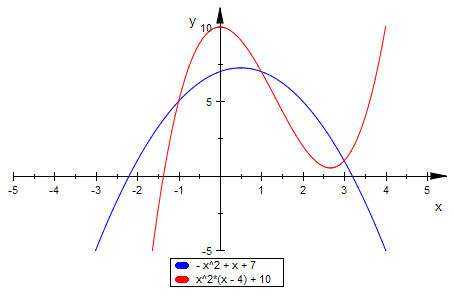
Behauptung: Beide Kurven haben im Intervall x0 bis x2 denselben Intergalwert.
Betrachtung der beiden Integrale
int(p3(x), x=x0..x2);
int(p2(x), x=x0..x2);
![]()
![]()
Sie sind gleich, da der Kepler-Wert für die Parabel exakt ist, ist er hier auch für p3 exakt.
Dass dies immer so ist, sieht man an der Differenzfunktion:
plotfunc2d(p2(x),p3(x),p3(x)-p2(x), ViewingBoxYRange=-5..10)
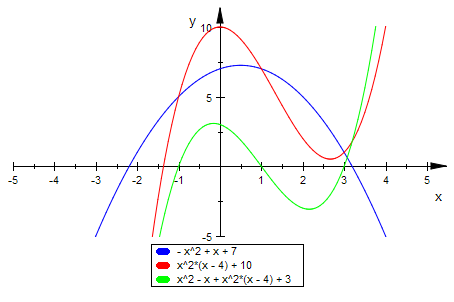
Da die innere Stützstelle nach Konstruktion immer die Mitte ist, hat das Differenz-Polynom
stets seinen Wendepunkt auf der x-Achse und man integriert es immer von rechter bis ganz linker Nullstelle. Dieses Integral ist immer Null. Daher heben sich immer die beiden Flächen auf, bei denen
p3 über bzw. unter der Parabel p2 liegt. q.e.d.
Also:
Für Polynome 3. Grades arbeitet die Kepler-Regel exakt.