P:=x->p*(1-p)^(x-1)
![]()
Stochastische Prozesse
GeometrischeVerteilung und Exponentialverteilung
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, April Update April 08
http:haftendorn.uni-lueneburg.de www.mathematik-verstehen.de
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
delete p:
P:=x->p*(1-p)^(x-1)
![]()
Oben steht eine Geometrische Verteilung P(X=x)=p*(1-p)^(x-1)
Sie hat den Erwartungswert 1/p
sum(x*P(x), x=1..infinity)
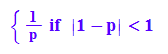
------------------------------------------
Unten steht eine die Dichte einer Exponentialverteilung,
ebenfalls mit dem Erwartungswert 1/p
f:=x->p*E^(-p*x)
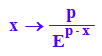
int(x*f(x), x=0..infinity)
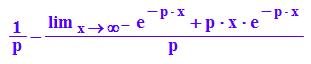
Der Limes ist 0, also Erwartungswert = 1/p
p:=1/30:
plotfunc2d(P(x),f(x),x=0..40)
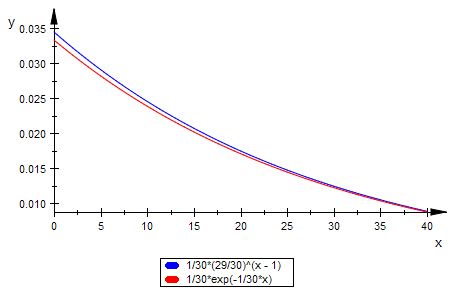
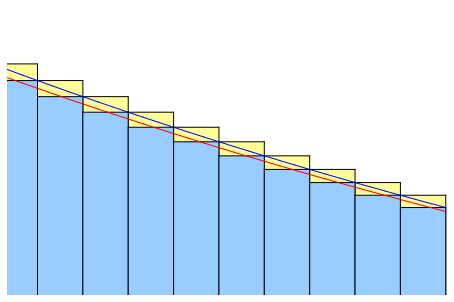
Blau ist die Randkurve der Geometrischen V. Rot ist die Exponentialverteilung.
Ich verwende Riemannsche Summen-Balken um Arbeit zu sparen. Man kann immerhin erkennen,
dass ber P nur die Balken gemeint sind, genauer, der MittelBalken jeweils.
Pg:=plot::Function2d(P(x),x=0..40, Color=[0,0,1]):
pg:=plot::Function2d(f(x),x=0..40, Color=[1,0,0]):
Pb:=student::plotRiemann(P(x),x=0..40,40):
plot(Pb,pg)
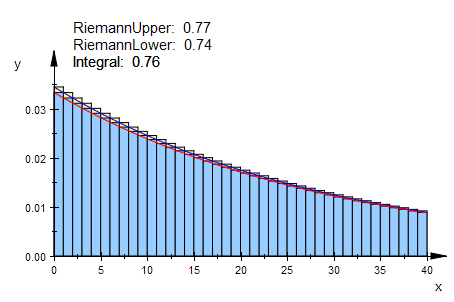
Nimmt man einen Ausschnitt bei x etwa 35 so sieht man brauchbare Übereinstimmung.
plot(Pb,pg)