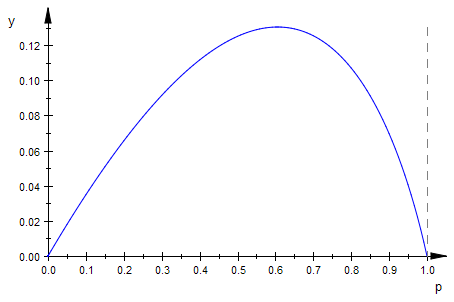
HW:=matrix([[p,1-p],[1-q,q]]);
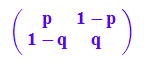
Handwerker und geometrische Verteilung
Prof. Dr. Dörte Haftendorn MuPAD 4 Nov. 07 http://haftendorn.uni-lueneburg.de
#############################################################
Markowkette mit zwei Zuständen, Handwerkerbeispiel,
siehe zughörige pdf-Seite
Nun aber allgemein durchgeführt. Achtung hier ist nicht notwendig q gleich 1-p.
HW:=matrix([[p,1-p],[1-q,q]]);
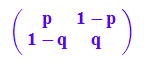
Übergangsmatrix
HW^2
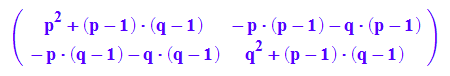
expand(%)
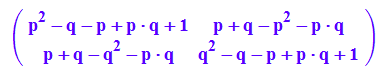
HW71:=(HW|p=0.7)|q=0.9

Aus der Eigenvektorberechnung auf der pdf-Seite ergibt sich:
Q:=3:
vh:=matrix([[1/(1+Q),1/(1+1/Q)]])
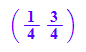
Dieses soll also der Eigenvektor sein:
vh*HW71
![]()
Er ist es tatsächlich.
HW71^10

Das zeigt sich auch beim Potenzieren der Übergangsmatrix.
matrix([[0,1]])*HW71^20
![]()
Hier zeigt sich übrigens, dass man mit Rechner Eigenvektoren leicht durch
hinreichend hohe Potenzen der Übergangsmatrix bekommt.
#############################################################
Simulation für die mittlere Wartezeit
Wahrscheinlichkeit für 1 sei 25%.
ar:=random(1..4):
ar() $ k=1..20
![]()
Mittlere Wartezeit auf eine 1. Durch Auszählen gewonnen.
(2+4+7+2+3)/5, "=",float((2+4+7+2+3)/5)
![]()
Geometrische Verteilung
Theoretisch wird die Wartezeit auf ein Ereignis, das mit Wahrscheinlichkeit p eintritt,
modelliert durch eine "Geometrische Verteilung", wie man sich leicht am
Baumdiagramm klarmacht.
P(T=k)=p*(1-p)^k
p*hold((1-p))^k $ k=0..5
![]()
Dieses ist eine unendliche geometrische Folge, ihre Summe ist
p*1/(1-(1-p))
![]()
Darum ist dies die Verteilung der Wartezeit.
p:=0.25:
plot(plot::Bars2d([p*(1-p)^k $ k=0..10]))
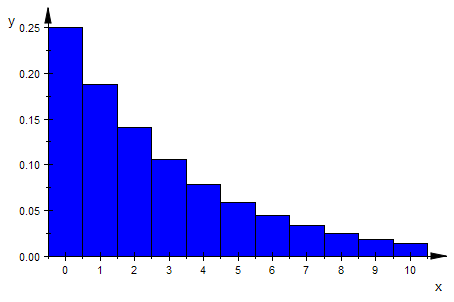
Die mittlere Wartezeit kann man überlegen: Wenn die W. 25% ist kommen auf 100 Takte
25 Erfolge. Verteilt man die gleichmäßig auf die 100, muss man im Mittel 4 Takte
auf einen Erfolg warten, allgemein 1/p Takte.
Auf ein p-Ereignis muss man im Mittel 1/p Takte warten.
Das ergibt sich auch durch die theoretische Erwartungswertberechnung.
p*(1-p)^(1/p)
![]()
Dies ist die Wahrscheinlichkeit, dass der Erwartungswert der Wartezeit eintritt.
%|p=0.25
![]()
plotfunc2d(p*(1-p)^(1/p),p=0..1)