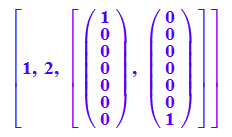SPQ:=matrix([[1,0,0,0,0,0,0],
[q,0,p,0,0,0,0],
[0,q,0,p,0,0,0],
[0,0,q,0,p,0,0],
[0,0,0,q,0,p,0],
[0,0,0,0,q,0,p],
[0,0,0,0,0,0,1]]);

Markow-Spiel
Prof. Dr. Dörte Haftendorn MuPAD 4 Dez. 06 http://haftendorn.uni-lueneburg.de
#####################################################################
Spiel mit unsymmetrischer Münze
Anton und Berta werfen eine unsymmetrische Münze mit P(Kopf)=p. Wennn Kopf fällt, zahlt Anton an Berta
1€ anderenfalls bekommt er 1 € von Berta. Beim Start hat Anton 4 € und Berta 2 €, das Spiel endet,
wenn einer von beiden Pleite ist.
Spezielle Untersuchung dieses Spielbeispiels aus dem Buch:
Die Übergangsmatrix ist dabei aufgebaut nach den Zuständen in Antons Geldtasche.
Insgesamt existieren im Spiel 6 €, also Zustände 0,1,2,3,4,5,6 für Anton. Ebenso ist
es für Berta. Die 1en in der Matrix signalisieren, dass Anton aus dem Zustand
0 € und aus 6 € nicht wieder herauskommt.
Gliederung:
1. Modellierung mit Übergangsmatrix,
2. Durchführung für p=1/2.
3. Durchführung für p=0.3.
4. Ausprobieren, wann das Spiel trotz Start mit 4 € gerecht ist.
5. Weitere theoretische Untersuchung
6. Bestimmung des Erwartungswertes der Spieldauer.
6 a) für p=0.3
6 b) Prozedur und Ausprobieren mit mehreren p.
7. Eigenvektor
#########################################
1. Modellierung
Das Spiel startet in Zeile 5, er hat nämlich 4 €
SPQ:=matrix([[1,0,0,0,0,0,0],
[q,0,p,0,0,0,0],
[0,q,0,p,0,0,0],
[0,0,q,0,p,0,0],
[0,0,0,q,0,p,0],
[0,0,0,0,q,0,p],
[0,0,0,0,0,0,1]]);

delete p,q:p,q
![]()
SP:=SPQ|q=1-p

2. Sonderfall: Spiel mit üblicher Münze
//p:=0.5; q:=1-p;
SPD:=SP|p=0.5

SPD^2

SPD^30

Man sieht noch nicht so recht, dass nur in der ersten und letzten Spalte größere Wahrscheinlichkeiten übrigbleiben.
Die Nullen sagen, dass man in Schritt 30 den entsprechenden Zustandsübergang nicht machen kann.
float(SPD^501)

Beim Start in Zustand 5 (mit 4 € ) wird bei p=1/2 Anton also mit 33,333% Wahrscheinlichkeit in Zustand 1, (d.h 0 €) landen, also verlieren.
start:=matrix([[0,0,0,0,1,0,0]]): start*SPD^500
![]()
#######################################################
2. Durchführung für Kopf-Wahrscheinlichkeit 30%.
delete p:
(SP3:=SP|p=0.3)

(SP3)^k $k=2..3

Man sieht noch nicht so recht, dass nur in der ersten und letzten Spalte größere Wahrscheinlichkeiten übrigbleiben.
TH:=start*SP3^100
![]()
Beim Start in Zustand 5 (mit 4 € ) wird bei p=0.3 Anton also mit 82,1% Wahrscheinlichkeit in Zustand 1, (d.h 0 €) landen, also verlieren.
#######################################################################
4. Die Frage ist, Welche Kopf-Wahrscheinlichkeit gerade diesen Vorteil ausgleicht.
Experimentelle Lösung:
(SP4:=SP|p=0.4):
start*SP4^1000
![]()
(SP4:=SP|p=0.44):
start*SP4^1000
![]()
(SP4:=SP|p=0.440137):
start*SP4^1000
![]()
Mit etwa p=44% für Kopf sind bei dieser Startgeldaufteilung die Chancen für beide etwa gleich.
Dieter Riebesehl hat berechnet
pgleich:=(2*sqrt(2+sqrt(5))-1-sqrt(5))/2; float(%)
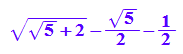
![]()
#####################################################################
5. Weitere theoretische Untersuchung, Buch Waldmann, Stocker: Stoch. Prozesse
delete p:
SP^8
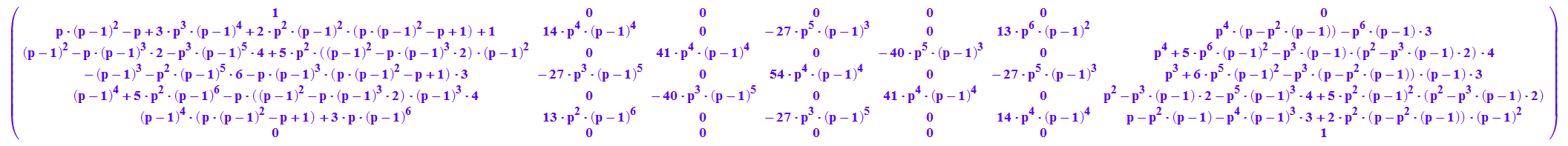
Für das Element sp51 von SP^8 schlägt das Buch vor:
expand((1-p)^4+4*p*(1-p)^5+13*p^2*(1-p)^6);
expand((SP^8)[5,1]); /* meins */
expand((start*SP^8)[1]); /* meins */
![]()
![]()
![]()
und das ist dasselbe.
############################################
6. Bestimmung der Erwartungswerte
Zunächst für p=0.30
n:=80:
pkg:=((SP3^k)[5,1]+(SP3^k)[5,7] )$ k=1..n
![]()
Dies sind die Wahrscheinlichkeiten , dass bis zum k-ten Schritt bei Start mit 4 € ein Endzustand erreicht ist.
pkgd:=pkg[i]-pkg[i-1] $i=2..n
![]()
Dies sind ab i=2 die Wahrscheinlichkeiten, dass das Spiel nach genau i Schritten einen Endzustand erreicht hat.
In einem ungeraden Schritt kann man den Endzustand nicht erreichen.
nops(pkgd);
sum(pkgd[i],i=1..nops(pkgd))
![]()
![]()
Die Summe dieser Wahrscheinlichkeiten ist annähernd 1.
Damit liegt eine Verteilung der Zufallsgröße Spielzeit vor.
Der Erwartungswert wird berechnet, indem man mit die Werte der Zufallsgröße mit den
Wahrscheinlichkeiten, mit denen sie angenommen werden, multipliziert und diese Produkte addiert.
erw:=sum((i+1)*pkgd[i] , i=1..nops(pkgd));
![]()
Bei p=0.3 ist das Spiel im Mittel nach 7.3 Würfen zuende.
delete p:
erwart:=proc(pp,n)
local A, k,pkg,pgkd, erw, vert;
begin
(A:=SP|p=pp);
pkg:=((A^k)[5,1]+(A^k)[5,7] )$ k=1..n;
pkgd:=pkg[i]-pkg[i-1] $i=2..n;
vert:=sum(pkgd[i],i=1..nops(pkgd));
erw:=sum((i+1)*pkgd[i] , i=1..nops(pkgd));
print(Unquoted,"p=",pp," Verteilung? (bei n=",n,") Sum=",vert);
print(Unquoted,"mittl. Spieldauer (Würfe): ",erw):
end_proc:
Praktisch ist die Zusammenfassung in einer Prozedur:
erwart(0.01,80),erwart(0.2,80),erwart(0.3,100),
erwart(0.44,100),erwart(0.5,100),erwart(0.8,80),erwart(0.95,80)
p=, 0.01, Verteilung? (bei n=, 80, ) Sum=, 1.0
mittl. Spieldauer (Würfe): , 4.081007977
p=, 0.2, Verteilung? (bei n=, 80, ) Sum=, 1.0
mittl. Spieldauer (Würfe): , 6.043956044
p=, 0.3, Verteilung? (bei n=, 100, ) Sum=, 0.9999999998
mittl. Spieldauer (Würfe): , 7.32124528
p=, 0.44, Verteilung? (bei n=, 100, ) Sum=, 0.9999996884
mittl. Spieldauer (Würfe): , 8.352512266
p=, 0.5, Verteilung? (bei n=, 100, ) Sum=, 0.9999994337
mittl. Spieldauer (Würfe): , 7.999938837
p=, 0.8, Verteilung? (bei n=, 80, ) Sum=, 1.0
mittl. Spieldauer (Würfe): , 3.296703297
p=, 0.95, Verteilung? (bei n=, 80, ) Sum=, 1.0
mittl. Spieldauer (Würfe): , 2.222171208
Interessant ist, dass beim gerechten Spiel die mittlere Spieldauer am größten ist.
###############################################################
Anmerkung: Im Buch Waldmann, Stocker wird mit viel formalem Aufwand und wenig Begründung
ein Gleichungssystem hergeleitet, das diesen Erwartungswert liefert. Da man letzlich doch numerisch arbeiten
muss, ist -zumindest schulisch- diese Berechnung entschieden sinnvoller.
n muss man so groß wählen, dass sie Summe der W. fast 1 ist. Davon abgesehen ist diese
auch eine theoretische Lösung.
----------------------------------------------------------------------------------------------------------------
Davon zu unterscheiden sind die Betrachtung von Simulationen.
Das ist hier (noch) nicht vorgesehen.
----------------------------------------------------------------------------------------------------------------
7. Berechung der Eigenvektoren
SP

Dies war die Übergangsmatrix, Bestimmung der Eigenwerte:
linalg::eigenvalues(SP)
![]()
Der zweite Eigenwert ist 1. Er kommt für die stochastische Deutung infrage.
Es sind 6 Eigenwerte, damit hat jeder nur einen Eigenvektor (bis auf Länge).
Unten ist angefügt, dass 1 ein doppelter Eigenwert ist.
Stochastisch ist es wegen der Normierung ein höchstens eindimensinaler Eigenraum.
v:=matrix([[v1,v2,v3,v4,v5,v6,v7]])
![]()
solve(v*SP=v,{v1,v2,v3,v4,v5,v6,v7})
![]()
Die Bestimmung des zugehörigen Eigenvektors hat
vv:=matrix([[v1,0,0,0,0,0,1-v1]]);
vv*SP
![]()
![]()
Die Menge aller Punkte mit x1+x2+ x3+x4+ x5+x6+ x7=1 ist eine Hyperebene im
7-dimensionalen Raum. Mit der Beschränkung 0<= xi <=1 ist es das Innere des Hyper-7-Ecks im
vollständig positiven Koordinatengebiet.
Wenn bei der Eigenvektorberechnung durch die Normierung keine Freiheit mehr bleibt, erhält man den
Punkt, an dem die durch den Eigenvektor gebildete Ursprungsgerade die Hyperebene durchstößt.
Hier aber bleibt eine Variable unbestimmbar.
Das heißt, der eben berechnte Eigenvektor ist zu sehen als Strecke, die in dem Hyper-7-eck enthalten ist.
Sie hat den Aufpunkt (0,0,0,0,0,0,1) und den Richtungsvektor (1,0,0,0,0,0,-1)
Fazit: Alle Zeilen der SP^n haben für jedes p die Gestalt dieser Eigenvektoren, jede Zeile aber einen anderen.
Der Eigenvektor (0.5,0,0,0,0,0,0.5) besagt, dass jemand, der mit 0 € oder 6€ ins "Spiel" eintritt, verbleibt in dem
Zustand 0€ oder 6 € zu haben, denn das beendete Spiel ändert gar nichts mehr.
(linalg::eigenvectors(linalg::transpose(SPQ))|q=(1-p))[3]