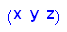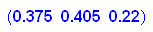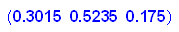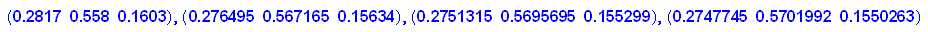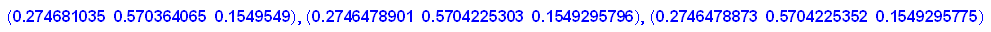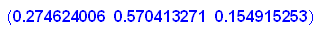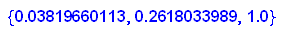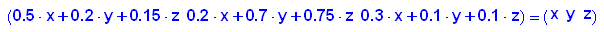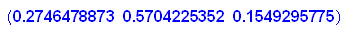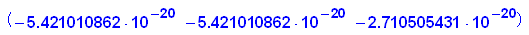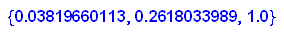markow3x3

Markow-Ketten mit drei Zuständen
Stochastik mit MuPAD,
Prof. Dr. Dörte Haftendorn 23.11.04 Version vom 23.11.04
------------------------------------Evaluiere alle Eingaben-----------------------------------------------

Drei Zustände: Sonne, Nebel, Regen
Die Prozentsätze geben an, mit welcher Wahrscheinlichkeit morgen der
betreffende Zustand eintritt.
Also:
Wenn heute Sonne ist, dann ist mit 50% Wahrscheinlichkeit
auch morgen Sonne, mit 20 % W. ist Nebel, mit 30 % W. ist Regen
Wenn heute Nebel ist, dann ist mit 20% W. morgen Sonne, mit 70% W. wieder Nebel, mit 10% W. Regen,
Wenn heute Regen ist, dann ist mit 15% W. morgen Sonne, mit 75% W. Nebel, mit 10% W. wieder Regen,
nur mit 10% W. kommen sie morgen.

Dieser Zusammenhang wird durch die Übergangsmatrix beschrieben:

A := matrix([[0.5, 0.2,0.3], [0.2,0.7, 0.1], [0.15,0.75,0.1]])

A heißt "stochastische Matrix".
Die Zeilensummen stochastischer Matrizen müssen 1 sein.
Entsprechend gibt es auch "Zustandsvektoren" als stochastische Vektoren.
Sie sind Zeilenvektoren mit Zeilensumme 1.
(0.6 0.3 0.10) bedeutet dann, dass heute mit 60% Wahrscheinlichkeit Sonne ist,
mit 30% W. Nebel und mit 10% W. Regen.
Es ist die Verteilung der Zustände heute.
Wie sieht dann die Verteilung der Zustände morgen aus?

v:=(x,y,z)->matrix([[x,y,z]]): v(x,y,z)

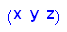
Es wird günstigerweise ein Vektor v als Funktion von x und y definiert.

v(0.6,0.3,0.1)

Zur Beantwortung der Frage muss man v mit A multiplizieren:

v(0.6,0.3,0.1)*A

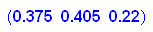
Morgen ist dann die Verteilung der Zustände 37,5% für Sonne, 22,5% für Nebel und 40% für Regen.

v(0.6,0.3,0.1)*A^2

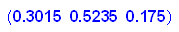
Dies ist die Verteilung übermorgen.

v(0.6,0.3,0.1)*A^i $ i=3..6

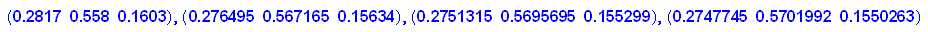
Dieses in den folgenden Tagen. Nun betrachten wir Wochen:

v(0.6,0.3,0.1)*A^(i*7) $ i=1..3

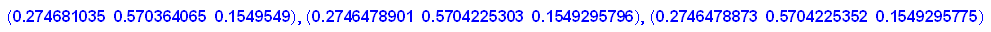
Da scheint sich ja eine stabile Verteilung zu bilden. Wie versuchen:

v(0.2746,0.57042253,0.15493)*A

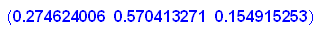
Das ist offenbar nicht ganz richtig geraten.
Das heißt: auf Dauer wird es vielleicht eine Verteilung geben, wie bekommt man die?
Der gesuchte Vektor (xe, ye,ze) ist ein Eigenvektor der Matrix A. Wenn man ihn mit A multipliziert,
kommt muss er selbst wieder herauskommen.
Allgemein heißt ein Vektor v Eigenvektor zum Eigenwert k, wenn gilt v*A=k*v.
Der obige Vektor muss also Eigenvektor zum Eigenwert k=1 sein.
Eigenwerte und Eigenvektoren kann man "von Hand" oder mit CAS bestimmen.
Eigenwerte "von Hand" siehe ganz unten.
Erst mit CAS, hier mit MuPAD:

linalg::eigenvalues(A)

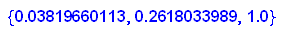
1 ist also tatsächlich ein Eigenwert.
Der zugehörige Eigenvektor erfüllt:

v(x,y,z)*A=v(x,y,z)

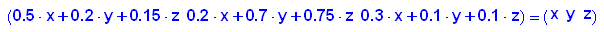
Das war mit Abschreiben. Automatisch:

grenz:=solve([op(v(x,y,z)*A,1)=x,op(v(x,y,z)*A,2)=y,op(v(x,y,z)*A,3)=z,x+y+z=1],[x,y,z])

Da ist als die stabile Zustandsverteilung herausgekommen.

gvx:=op(op(op(grenz),1),2);gvy:=op(op(op(grenz),2),2);gvz:=op(op(op(grenz),3),2);

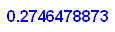
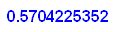
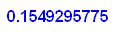
gv:=matrix([[gvx,gvy,gvz]])

gv*A

gv*A^5

---------------------------------------------------------------------------------------------------------------------------------
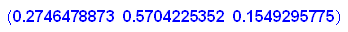
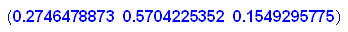
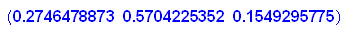
Allgemeine Betrachtungen:

Aalg:=matrix([[1-p2-p3,p2,p3], [q1,1-q1-q3,p3],[r1,r2,1-r1-r2]])

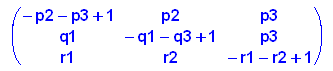
//linalg::eigenvalues(Aalg): //riesige Terme

Alle stochastischen 3x3-Matrizen haben den Eigenwert 1???????.

Das Eigenvektorkonzept ist für Spaltenvektoren von rechts konzipiert.
Darum kippen wir die Matrix und das Ergebnis.

//alles:=linalg::eigenvectors(linalg::transpose(Aalg)) //zu groß, die Terme

Eigenvektoren sind beliebig skalierbar.
Allgemein ist da offenbar zu schwierig
Die anderen Eigenvektoren sind in diesem Thema nicht deutbar.
---------------------------------------------------------------------------------------------------------------
Allgemein

Aalg^2

//Aalg^3:

------------------------------------------------------------------------------------------------------
Potenzen von A

A^2

A^i $ i=1..4

A^i $ i=5..7

AG:= matrix([[op(gv)],[op(gv)],[op(gv)]])

gv*AG-gv

---------------------------------------------------------------------------------------------------------------------
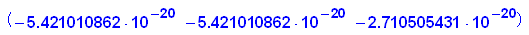
Tatsächlich konvergiert die Folge A^n gegen die Matrix,
die aus der stabilen Verteilung als drei Zeilenvektoren gebildet wird.

---------------------------------------------------------------------------------------------------------
Eigenwerte "von Hand":
v*A=k*v soll gelten, k heißt dann Eigenwert.
Also muss v*A-k*v=0 sein. Damit man v ausklammern kann, muss man die
Einheitsmatrix EE zuhilfe nehmen.
v*(A-k*E)=0 . Dies ist eine Vektorgleichung, bei der der Nullvektor herauskommen soll,
man sagt auch: es ist ein homogenes Gleichungssystem.
Nichttriviale Lösungen kommen aber nur dann zustande, wenn die Determinante
der Matrix A-k*EE =0 ist.
Bei 3x3-Matrizen ist die Determinate nach der Sarrusschen Regel zu berechnen.

EE:=A^0

A-k*EE

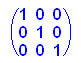
linalg::det(A-k*EE) //Charakteristisches Polynom

solve(%=0,k)

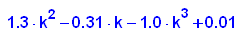
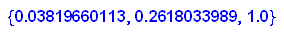
Die Nullstellen des Charakteristischen Polynoms sind die Eigenwerte.
Tatsächlich ist ein Eigenwert 1

Az := matrix([[5/10, 2/10,3/10], [2/10,7/10, 1/10], [15/100,75/100,1/10]])

Az-k*Az^0

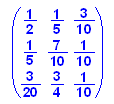
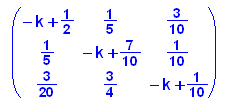
linalg::det(Az-k*Az^0) //Charakteristisches Polynom

solve(%=0,k)

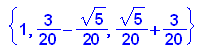
zgrenz:=solve([op(v(x,y,z)*Az,1)=x,op(v(x,y,z)*Az,2)=y,op(v(x,y,z)*Az,3)=z,x+y+z=1],[x,y,z])

142*(Az^20)


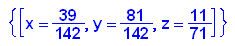
               array(1..3, 1..3,
                 (1, 1) = 3900000000028720848193/100000000000000000000,
                 (1, 2) = 8099999999949338376159/100000000000000000000,
                 (1, 3) = 68750000000685649239/3125000000000000000,
                 (2, 1) = 3899999999990677018161/100000000000000000000,
                 (2, 2) = 8100000000016445106211/100000000000000000000,
                 (2, 3) = 549999999998219468907/25000000000000000000,
                 (3, 1) = 974999999995852823289/25000000000000000000,
                 (3, 2) = 4050000000014630675607/50000000000000000000,
                 (3, 3) = 219999999998732735563/10000000000000000000
               )

Hier könnte man mit scharfem Hinsehen die Zähler herauskriegen.

gzvx:=op(op(op(zgrenz),1),2);gzvy:=op(op(op(zgrenz),2),2);gzvz:=op(op(op(zgrenz),3),2);

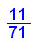
gzv:=matrix([[gzvx,gzvy,gzvz]])

gzv*Az

Also ist gzv wirklich Grenzverteilung.