A:=matrix([[0.5,0.2,0.3],
[0.2,0.7,0.1],
[0.15,0.75,0.1]]);

Homogene Markowketten
Prof. Dr. Dörte Haftendorn MuPAD 4, Nov. 06 http://haftendorn.uni-lueneburg.de
Wetter in Bad Markstein
A:=matrix([[0.5,0.2,0.3],
[0.2,0.7,0.1],
[0.15,0.75,0.1]]);

Übergangsmatrix für das Wetter in Bad Markstein,
Zustände Sonne, Nebel, Regen
s:=matrix([[1,0,0]])
![]()
Startverteilung, Mathix kommt am Freitag bei Sonne an.
s*A
![]()
Wetterverteilung für Samstag, mit 50% W. ist Sa Sonne.
s*A*A
![]()
Wetterverteilung für Sonntag, mit 33,5% W. ist Sonntag Sonne.
Die Wetterverteilung der nächsten 3 Tage,
s*A^k $k=3..5
![]()
s*A^20, (s*A^20)*A
![]()
Die Wetterverteilungen am 20. und 21. Tag unterscheideden sich gar nicht.
Das ist die stationäre Wetterverteilung von Bad Markstein.
Hier ist sie gefunden durch Potenzieren von A.
Man kann sie aber zu bestimmen versuchen:
v:=matrix([[v1,v2,v3]]);
![]()
Aufstellen einer Eigenvektor-Gleichung.
solve(v*A=v,{v1,v2,v3});
![]()
Eigenvektoren sind nur bis auf einen Faktor bestimmt. Der ist noch durch die Normierung von v
zu eliminieren. Als Wetterverteilung ist v eine "stochastischer Vektor", hat also Komponentensumme1.
float(solve([v1 = 1.772727273*z, v2 = 3.681818182*z, v3 = z,
v1+v2+v3=1],{v1,v2,v3}));

Ich hatte da auch von Hand gerechnet, offenbar sind das dieselben Zahlen.
vv:=matrix([[op(float({39/142,81/142,11/71}))]]);
![]()
Bei dieser Wetterverteilung, herrscht einen Tag später dieselbe Wetterverteilung.
vv*A
![]()
A^20

Betrachtet man A^20 selbst, so sieht man, dass der stationäre Verteilungsvektor
in allen Zeilen steht.
############################################################
M:=1/6*matrix([[2,3,1],[2,3,1],[2,3,1]]);
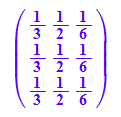
M^2
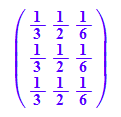
Stochastische Matrizen mit 3 gleichen Zeilen sind idempotent,
d.h. M^2=M
M:=1/(a1+a2+a3)*matrix([[a1,a2,a3],[a1,a2,a3],[a1,a2,a3]]);

simplify(M^2)

#####################################################################
Spiel mit unsymmetrischer Münze ist jetzt eigene Datei.
Handwerker-Beispiel ist jetzt eigene Datei.