Warteschlangen
Prof. Dr. Dörte Haftendorn, Dez. 04 Version vom 12.12.04
lam Personen kommen im Mittel in Zeiteinheit Z an, z.B. 3 pro 1/4-Stunde.
my Personen werden im Mittel pro Zeiteinheit Z bedient, z.B. 4 pro 1/4-Stunde.

• delete lam, my:

• lam:=3:my:=4:

• rho:=lam/my  //rho heißt auch Auslastung 

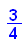
Übergangsmatrix

• A:=matrix([[1-lam,lam,    0,0], 
             [my,1-lam-my,lam,0], 
             [0,my,1-lam-my,lam], 
             [0,  0,my,1-lam-my]])

Eigentlich müsste es stets lam*h, my*h heißen mit einem h, das dann später immer kleiner gemacht werden
kann. Bei dem Problem, die Grenzverteilung zu bestimmen, fällt h dann aber heraus. Darum
wird auf das Mitziehen in den Termen verzichtet.

• A-A^0

Beginnt man das Gleichungssystem vA=v zu lösen, so
lässt man v1 zunächst in allen Gleichungen stehen .
Man merkt: v2= rho*v1 und v(n+1) =rho*v(n), also eine geometrische Folge mit Faktor rho.
v1 bestimmt man nun durch die Bedingung, dass v1+v2+v3+.....=1
sein muss, denn v muss stochastische Vektor sein, eine Verteilung beschreiben.
Wegen der Summe der geometrische Reihe führ das zu v1=1-rho.
Die Summe - und damit der Grenzwerteilung- existiert nur für
rho<1, also lam<my.

• v:=matrix([[1-rho,(1-rho)*rho,(1-rho)*rho^2,(1-rho)*rho^3]])

• v*A-v

• v*A

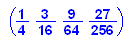
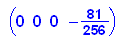
Es ist klar, dass die letzte Komponente hier nicht stimmt,
denn A ist ja hier keine unendliche Matrix und damit auch keine
echt stochastische Matrix.
Für das Folgende soll mit Dezimalzahlen gerechnet werden.

• rho:=lam/my*1.0;

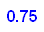
• vv:=matrix([(1-rho)*rho^k $ k=0..20])

Deutung: Mit 14% Wahrscheinlichkeit warten zu einem
beliebigen Zeitpunkt 2 Personen.
Die Verteilung der Zufsallgröße L=Länge der Warteschlange

• balken:=plot::bars(vv,Ticks=Automatic):plot(balken)
  

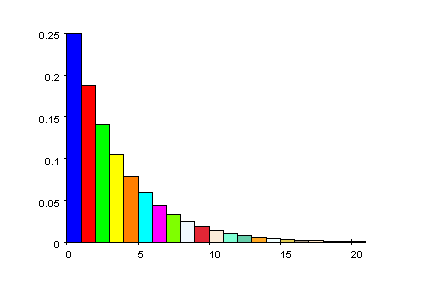
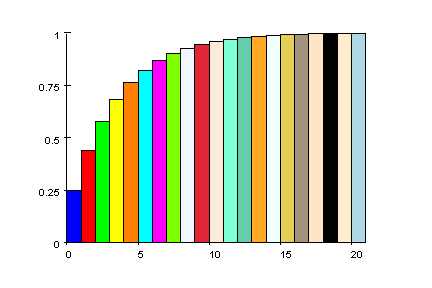
• cdf:=matrix([1-rho^(k+1) $ k=0..20]):

• cdf_sicht:=matrix([[k,1-rho^(k+1)] $ k=0..20])

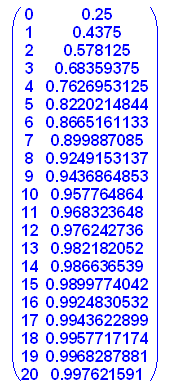
Deutung: mit etwa 90% Wahrscheinlichkeit warten
nicht mehr als 7 Personen. Aber in 1 % der
Fälle warten mehr als 15 Personen.

• balken_cum:=plot::bars(cdf,Ticks=Automatic):
  plot(balken_cum)

Diese Verteilung heißt (aus ersichtlichem Grund) "geometrische Verteilung".
Sie tritt auch auf bei dem Problem "Warten auf den ersten Erfolg".
Mit Wahrscheinlichkeit p habe man Erfolg in diesem "Takt", mit q keinen, Bernoulliverkette.
Die Zufallsvariable Z sei der Zahl der Takte, die verstreichen, bevor man Erfolg hat.
Im Takt Z+1 tritt der Erfolg dann aber ein.
P(Z=k)=p*q^k= p*(1-p)^k.
Hier ist offenbar p=1-rho, q=rho.

• //###################################

Erwarungswert, Standardabweichung und Kumulierte Verteilung
Unter Einsatz der Kenntnis über geometrische Folgen
ergeben sich recht elementar Parameter zu der Zufallesgröße
L= Anzahl der Wartenden.
E(L)=rho/(1-rho)=lam/(my-lam)
Var(L)=E(L)/(1-rho)
s(L)= sqrt(rho)/(1-rho)
P(L<=k)=1-rho^(k+1)

• Erw:=rho/(1-rho)

• Var:=Erw/(1-rho)

• s:=sqrt(Var)

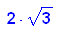
Quantile
ergeben aus der Ungleichung 1-rho^(k+1)<=alpha zu
k<=ln(1-alpha)/ln(rho) - 1

• [alpha*0.1,(ln(1-alpha/10.0))/ln(rho*1.0) - 1] $alpha=5..9

Deutung wie oben: in 90 % der Fälle warten bis zu 7 Personen.