Regression, Fehlerquadratsumme f(m,k)

Prof. Dr. Dörte Haftendorn - 16.10.2004

Nr. Name Definition Algebra
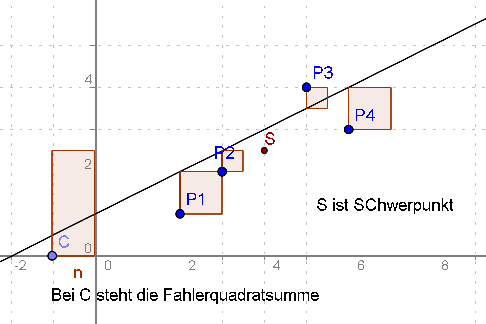
1 Punkt P1   P1 = (2, 1)
2 Punkt P2   P2 = (3, 2)
3 Punkt P3   P3 = (5, 4)
4 Punkt P4   P4 = (6, 3)
5 Zahl m   m = 0.5
6 Zahl k   k = 1
7 Funktion g g(x) = m x + k g(x) = 0.5 x + 1
8 Zahl xquer (x(P1) + x(P2) + x(P3) + x(P4)) / 4 xquer = 4
9 Zahl yquer (y(P1) + y(P2) + y(P3) + y(P4)) / 4 yquer = 2.5
10 Punkt S (xquer, yquer) S = (4, 2.5)
11 Zahl fmk (y(P1) - m x(P1) - k)² + (y(P2) - m x(P2) - k)² + (y(P3) - m x(P3) - k)² + (y(P4) - m x(P4) - k)² fmk = 2.5
12 Punkt R1 (x(P1), g(x(P1))) R1 = (2, 2)
13 Punkt R2 (x(P2), g(x(P2))) R2 = (3, 2.5)
14 Punkt R3 (x(P3), g(x(P3))) R3 = (5, 3.5)
15 Punkt R4 (x(P4), g(x(P4))) R4 = (6, 4)
16 Strecke r1 Strecke[R1, P1] r1 = 1
17 Strecke r2 Strecke[R2, P2] r2 = 0.5
18 Strecke r3 Strecke[R3, P3] r3 = 0.5
19 Strecke r4 Strecke[R4, P4] r4 = 1
20 Fünfeck P Fünfeck P1, R1, R1 + (r1, 0), P1 + (r1, 0), P1 P = 1
20 Strecke p1 Strecke[P1, R1] von Fünfeck P p1 = 1
20 Strecke c Strecke[R1, R1 + (r1, 0)] von Fünfeck P c = 1
20 Strecke r1 + (r1, 0) Strecke[R1 + (r1, 0), P1 + (r1, 0)] von Fünfeck P r1 + (r1, 0) = 1
20 Strecke p1 + (r1, 0) Strecke[P1 + (r1, 0), P1] von Fünfeck P p1 + (r1, 0) = 1
20 Strecke d Strecke[P1, P1] von Fünfeck P d = 0
21 Fünfeck Q Fünfeck P2, R2, R2 + (r2, 0), P2 + (r2, 0), P2 Q = 0.25
21 Strecke p2 Strecke[P2, R2] von Fünfeck Q p2 = 0.5
21 Strecke e Strecke[R2, R2 + (r2, 0)] von Fünfeck Q e = 0.5
21 Strecke r2 + (r2, 0) Strecke[R2 + (r2, 0), P2 + (r2, 0)] von Fünfeck Q r2 + (r2, 0) = 0.5
21 Strecke p2 + (r2, 0) Strecke[P2 + (r2, 0), P2] von Fünfeck Q p2 + (r2, 0) = 0.5
21 Strecke f Strecke[P2, P2] von Fünfeck Q f = 0
22 Fünfeck R Fünfeck P3, R3, R3 + (r3, 0), P3 + (r3, 0), P3 R = 0.25
22 Strecke p3 Strecke[P3, R3] von Fünfeck R p3 = 0.5
22 Strecke h Strecke[R3, R3 + (r3, 0)] von Fünfeck R h = 0.5
22 Strecke r3 + (r3, 0) Strecke[R3 + (r3, 0), P3 + (r3, 0)] von Fünfeck R r3 + (r3, 0) = 0.5
22 Strecke p3 + (r3, 0) Strecke[P3 + (r3, 0), P3] von Fünfeck R p3 + (r3, 0) = 0.5
22 Strecke i Strecke[P3, P3] von Fünfeck R i = 0
23 Fünfeck T Fünfeck P4, R4, R4 + (r4, 0), P4 + (r4, 0), P4 T = 1
23 Strecke p4 Strecke[P4, R4] von Fünfeck T p4 = 1
23 Strecke j Strecke[R4, R4 + (r4, 0)] von Fünfeck T j = 1
23 Strecke r4 + (r4, 0) Strecke[R4 + (r4, 0), P4 + (r4, 0)] von Fünfeck T r4 + (r4, 0) = 1
23 Strecke p4 + (r4, 0) Strecke[P4 + (r4, 0), P4] von Fünfeck T p4 + (r4, 0) = 1
23 Strecke l Strecke[P4, P4] von Fünfeck T l = 0
24 Punkt C Punkt auf xAchse C = (-1.03, 0)
25 Viereck U Viereck C, C + (1, 0), C + (1, fmk), C + (0, fmk) U = 2.5
25 Strecke n Strecke[C, C + (1, 0)] von Viereck U n = 1
25 Strecke c + (1, 0) Strecke[C + (1, 0), C + (1, fmk)] von Viereck U c + (1, 0) = 2.5
25 Strecke c + (1, fmk) Strecke[C + (1, fmk), C + (0, fmk)] von Viereck U c + (1, fmk) = 1
25 Strecke c + (0, fmk) Strecke[C + (0, fmk), C] von Viereck U c + (0, fmk) = 2.5

Erstellt mit GeoGebra