Vier-Feldertafeln
Prof. Dr. Dörte Haftendorn MuPAD 4 Jan 07 http://haftendorn.uni-lueneburg.de
###############################################################
Vier-Felder-Test nach Fisher
Es geht darum, ob zwei verschiedene Gruppen, hier Typ A und Typ B genannt,
bezüglich eines ja/nein-Merkmals E unterschiedlich sind.
Dein Einfachheit halber wird hier von Personen gesprochen.
Es werden n Personen untersucht, von denen a vom Typ A und b vom Typ B sind.
Nach der Befragnung haben e Personen das Merkmal E und ne haben es nicht.
zum Beispiel
Interessant ist nun, dass die Aufteilung der e Personen auf Typ A und B durchaus verschieden sein kann,
auch wenn die Gruppen bzgl. E eigentlich gleich sind.
Null-Hypothese H0: Die Gruppen unterscheiden sich nicht bzgl. Merkmal E.
Foschungshypthese H1: Typ A weist weniger E auf, also Typ B mehr (oder umgekehrt).
Man beobachtet eine Aufteilung von e
Ist nun , so ist gar nichts mehr zu untersuchen, das gehört sicher zu H0.
Weicht die Beobachtung deutlicher davon ab, so ist zu fragen, mit welcher Wahrscheinlichkeit unter H0
diese Tafel und weitere, die H1 noch mehr stützen, auftreten.
Es gibt Möglichkeiten ea Personen mit Merkmal E unter den a Personen vom Typ A "anzukeuzen".
Es gibt Möglichkeiten eb Personen mit Merkmal E unter den b Personen vom Typ B "anzukeuzen".
Es gibt Möglichkeiten e Personen mit Merkmal E unter den n Personen überhaupt "anzukeuzen".
Also ist der erste Summand der gesuchten Wahrscheinlichkeit
Ptafel:=(ea,a,eb,b)->binomial(a,ea)*binomial(b,eb)/binomial(a+b,ea+eb)
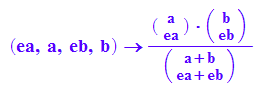
Durch diesen Formelaufbau sieht man Vieles, vor Allem, dass die Formel
symmetrisch in a und b ist. Also ist es egal, ob man die Hypothese auf A oder auf B bezogen
formuliert. Damit ist der Vier-Felder-Test immer einseitig formulierbar.
Ptafel(3,5,1,7), float(%)
![]()
Erstaunlicherweise ist die obige Tafel noch durchaus verträglich mit der Nullhypothese.
Hinreichend für eine Annahme von H1 ist
Ptafel(4,5,0,7); float(%)
![]()
![]()
Man hätte für eine Signifikanz also gebraucht:
alpha:=Ptafel(3,5,1,7)+Ptafel(4,5,0,7); float(%)
![]()
![]()
Das ganz oben angebene Ergebnis ist also nicht!!!!! signifikant. Man kann nicht behaupten,
dass das Merkmal E unter Typ A mehr verbreitet ist als unter B.
###################################################
Noch etwas Theorie als Hilfe für Zweifelsfälle:
Bei manchen Beispielen ist man sich nicht sicher, ob nicht E und Nicht-E die Typen bilden und
A und B die alternativen Merkmale sind.
Darüber braucht man nicht zu grübeln, denn wenn man die Formel für die Wahrscheinlichkeit mit
Fakultäten ausschreibt, folgt
PtafelTerm:=hold((a!*b!*e!*ne!)/((ea!*na!*eb!*nb!)*n!))

Man sieht: Unten ist eine Klammer aus den vier Innen-Elementen, der Zähler besteht aus den vier
Außen-Elementen, n! steht noch im Nenner. Also ist auch das symmetrisch, man muss nur darauf achten,
dass man die Binomialterme entweder nur aus Zeilenelementen oder nur aus Spaltenelementen baut.
Damit ist es auch wirkunkslos, wenn man Zeilen und Spalten vertauscht.
Aus didaktischer Sicht ist die oben verfolgte Begründung sinnvoller, da die Aufteilung in die Typen meist "vorgegeben" ist. Bücher sind da nicht immer geschickt.