fn := stats::normalQuantile(0, 1):
z1:=fn(0.995);
z5:=fn(0.975)
![]()
![]()
Binomialverteilung, Konfidenzintervall
(Würfeln, sechs oder nicht sechs)
Prof. Dr. Dörte Haftendorn 9.5.08 MuPAD 4 Update von 2011
http:haftendorn.uni.leuphana.de www.mathematik-verstehen.de
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
3. Konfidenzintervalle
4. Betrachtung der Verteilung
###################################################
3. Konfidenzintervall 5%-Niveau
fn := stats::normalQuantile(0, 1):
z1:=fn(0.995);
z5:=fn(0.975)
![]()
![]()
Konfidenzintervall-Ansatz
confAnsatz:=(k/n-p)^2=z5*p*(1-p)/n
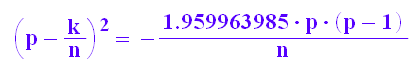
gl:=confAnsatz|{n=300,k=46.0}
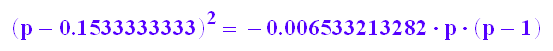
solve(gl,p)
![]()
Antwort: Aus dem Versuch mit n=300 erhält man ein 5%-Konfidenzintervall von
12,6% < p<18.5%
--------------------------------------
gl:=confAnsatz|{n=3000,k=527}

solve(gl,p)
![]()
Antwort: Aus dem Versuch mit n=3000 erhält man ein 5%-Konfidenzintervall von
16,6% < p<18,5%
--------------------------------------
gl:=confAnsatz|{n=30000,k=5065}

solve(gl,p)
![]()
Antwort: Aus dem Versuch mit n=30000 erhält man ein 5%-Konfidenzintervall von
16,58% < p<17,19%
--------------------------------------
Spielplatz
gl:=confAnsatz|{n=3000,k=500};
solve(gl,p)
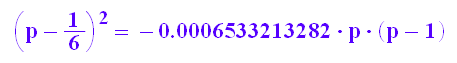
![]()
Andersherum, direkte Deutung der Binomialverteilung:
gl:=confAnsatz|{n=3000,k=500};
solve(gl,p)
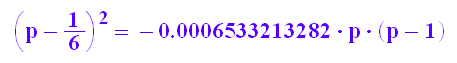
![]()
Bei 3000 Wurf liegen 95% solcher Simulationen in dem genannten Bereich.
##########################################################
##########################################################
4. Betrachtung der Verteilung und Quantile
nn:=300: pp:=1/6.0; my:=nn*pp;sig:=sqrt(nn*pp*(1-pp));
xmin:=my-4*sig;xmax:=my+4*sig;
![]()
![]()
![]()
![]()
![]()
bicdf:=stats::binomialCDF(nn,pp):
plotfunc2d(0.5,bicdf(x),0.975,0.025,x=xmin..xmax,
LegendVisible=FALSE)
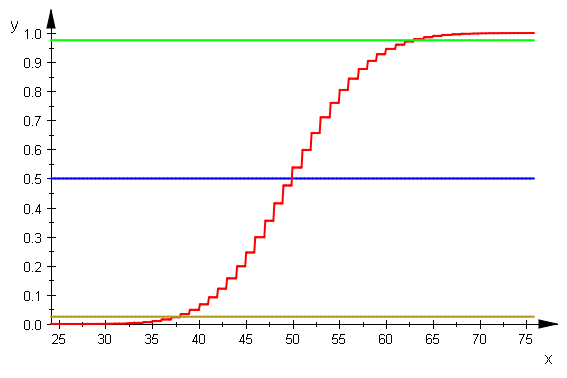
biHist ist eine Zeichenprozedur die bei Datei-Eigenschaften eingetragen ist un daher hier
aufgerufen werden kann
w=1 alle Werte, w=0 nur my, sigma
biHist(nn,pp,xmin,xmax,0)
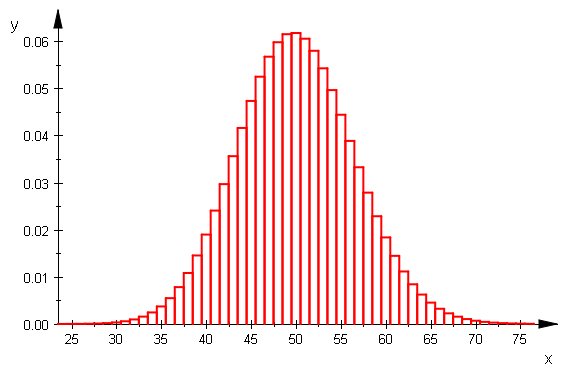
![]()
nn:=3000: pp:=1/6.0; my:=nn*pp;sig:=sqrt(nn*pp*(1-pp));
xmin:=my-4*sig;xmax:=my+4*sig;
![]()
![]()
![]()
![]()
![]()
bicdf:=stats::binomialCDF(nn,pp):
plotfunc2d(0.5,bicdf(x),0.9,0.1,x=xmin..xmax,
LegendVisible=FALSE)
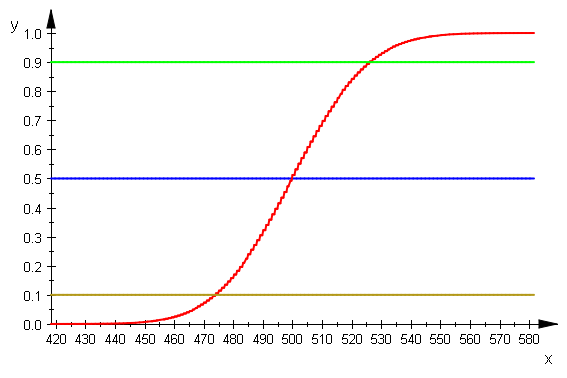
biHist ist eine Zeichenprozedur die bei Datei-Eigenschaften eingetragen ist un daher hier
aufgerufen werden kann
w=1 alle Werte, w=0 nur my, sigma
biHist(nn,pp,xmin,xmax,0)
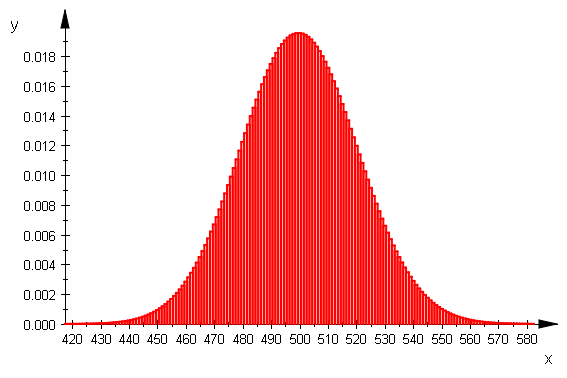
![]()
nn:=30000: pp:=1/6.0; my:=nn*pp;sig:=sqrt(nn*pp*(1-pp));
xmin:=my-4*sig;xmax:=my+4*sig;
![]()
![]()
![]()
![]()
![]()
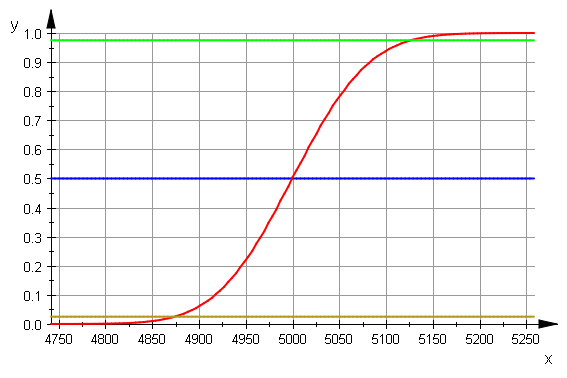
bicdf:=stats::binomialCDF(nn,pp):
plotfunc2d(0.5,bicdf(x),0.975,0.025,x=xmin..xmax,
LegendVisible=FALSE, GridVisible=TRUE)
biHist ist eine Zeichenprozedur die bei Datei-Eigenschaften eingetragen ist und daher hier
aufgerufen werden kann
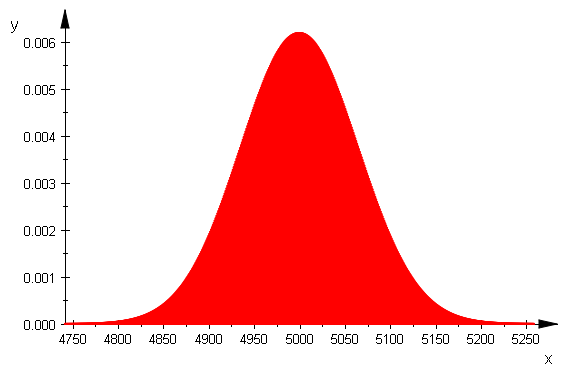
w=1 alle Werte, w=0 nur my, sigma
biHist(nn,pp,xmin,xmax,0)
![]()
Betrachtung der Quantile
Angabe der Intervalle, in denen 95% solcher Versuche
beim exakten Würfel wohl liegen werden
absolut und relativ
nn:=300: pp:=1/6.0:kf:=0.95:
f := stats::binomialQuantile(nn, pp):
grenzen:=f((1-kf)/2),f((1+kf)/2);
float(grenzen[1]/nn),float(grenzen[2]/nn);
![]()
![]()
nn:=3000: pp:=1/6.0:kf:=0.95:
f := stats::binomialQuantile(nn, pp):
grenzen:=f((1-kf)/2),f((1+kf)/2);
float(grenzen[1]/nn),float(grenzen[2]/nn);
![]()
![]()
Bestimmung eines 95%-Intervalls aus der Normalverteilung
z5;
gl:=confAnsatz|{n=3000,k=500};
solve(gl,p)
![]()
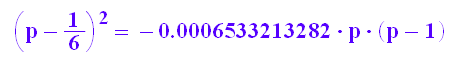
![]()
Bei 3000 Wurf liegen 95% solcher Simulationen in dem genannten Bereich.
Die Methoder mit den Binomialquantilen ist aber genauer.
##########################################################
nn:=30000: pp:=1/6.0:kf:=0.95:
f := stats::binomialQuantile(nn, pp):
grenzen:=f((1-kf)/2),f((1+kf)/2);
float(grenzen[1]/nn),float(grenzen[2]/nn);
![]()
![]()
Das heißt, dass man bei im Mittel bei einem von 20 solchen Versuchen
außerhalb des genannten Bereichs landen wird.