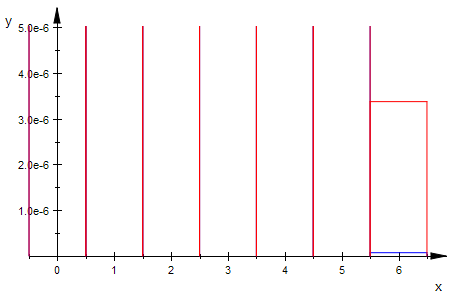
hypPDF:=(N,M,n,k)-> binomial(M,k)*binomial(N-M,n-k)/binomial(N,n)
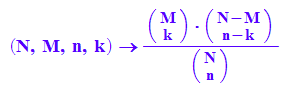
Hypergeometrische Verteilung
Prof. Dr. Dörte Haftendorn 9.5.08 MuPAD 4 Update vom 13. Juni 08
http:haftendorn.uni-lueneburg.de www.mathematik-verstehen.de
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Definition,Symmetrie, Histogramm, Vergleich mit Binomialverteilung, Lotto-Beispiel
N=Anzahl der Kugeln im Sack, M markierte, n werden gezogen ohne Zurücklegen.
X= Anzahk der markierten Kugeln in der Ziehung
X ist dann hypergeometrisch verteilt. P(X=k)= hypPDF(N,M,n,k)
hypPDF:=(N,M,n,k)-> binomial(M,k)*binomial(N-M,n-k)/binomial(N,n)
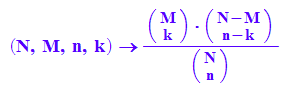
Wenn im Sack 6 weiße und 4 schwarze Kugeln sind, sind unter 3 ohne
Zurücklegen gezogenen Kugeln mit Wahrscheinlichkeit 1/2 genau zwei weiße.
hypPDF(10,6,3,2)
![]()
hypHist:=proc(N,M,n,kmin,kmax,w)
//w=1 alle Werte, w=0 nur my, sigma
local i,hypf,p,kmi,kma,li;
begin
hypf:=stats::hypergeometricPF(N,M,n):
p:=M/N;
kmi:=round(kmin): kma:=round(kmax):
i:=kmi:li:=[]:
werte:=[i,hypf(i)] $ i=kmi..kma;
for i from kmi to kma do
li:=li.[[i-0.5,0],[i-0.5,hypf(i)],[i+0.5,hypf(i)],[i+0.5,0]];
end_for;
histhy:=plot::Polygon2d(li,LineColor=[0,0,1]);
plot(histhy);
if w=1 then
return(matrix(float([werte])));
else return(float(["my",n*p]),
float(["sigma",sqrt(n*p*(1-p)*(N-n)/(N-1))]))
end_if;
end_proc:
Hypergeometrisch(Gesamtzahl, davon markierte, n ziehen, von , bis, anzeigen)
hypHist(N,M,n,von,bis,w)
Für w=1 werden alle Werte ausgeben, für w=0 nur my und sigma
Bild heißt histhy und ist auch außen erhältlich.
hypHist(10,6,3,0,3,1);
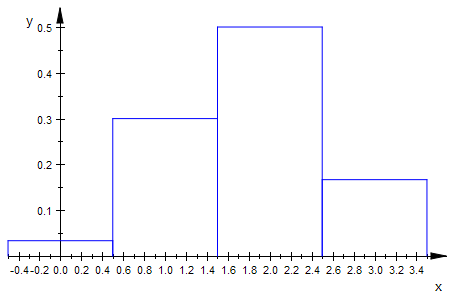

Symmetrieeigenschaft,
M und n kan man vertauschen
hypPDF(100,21,7,3);
hypPDF(100,7,21,3);
![]()
![]()
M!/(k!*(M-k)!)*(N-M)!/((n-k)!*(N-M-n+k)!)*n!*(N-n)!/N!
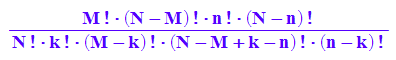
Man sieht, dass dieser Term in M und n symmetrisch ist.
hypHist(100,10,30,0,10,0);
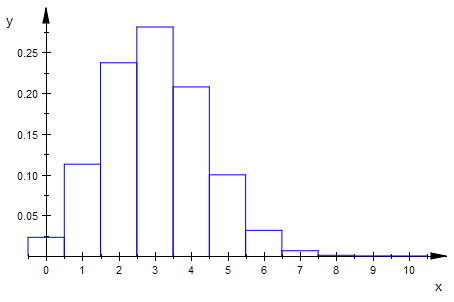
![]()
hypHist(100,30,10,0,10,0);
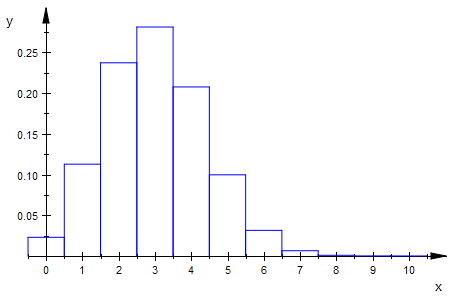
![]()
Vergleich mit der Binomialverteilung
Definition, die ein Histogamm passend zeichnet .
biHist:=proc(n,p,kmin,kmax,w)
//w=1 alle Werte, w=0 nur my, sigma
local i,bipf,kmi,kma,li;
begin
bipf:=stats::binomialPF(n,p):
kmi:=round(kmin): kma:=round(kmax):
i:=kmi:li:=[]:
werte:=[i,bipf(i)] $ i=kmi..kma;
for i from kmi to kma do
li:=li.[[i-0.5,0],[i-0.5,bipf(i)],[i+0.5,bipf(i)],[i+0.5,0]];
end_for;
histbi:=plot::Polygon2d(li,LineColor=[1,0,0]);
plot(histbi);
if w=1 then
return(matrix(float([werte])));
else return(float(["my",n*p]),
float(["sigma",sqrt(n*p*(1-p))]))
end_if;
end_proc:
biHist(n,p,kmin,kmax,w)
Für w=1 werden alle Werte ausgeben, für w=0 nur my und sigma
Das Bild heißt histbi und ist auch außen erhältlich.
biHist(10,0.3,0,10,0)
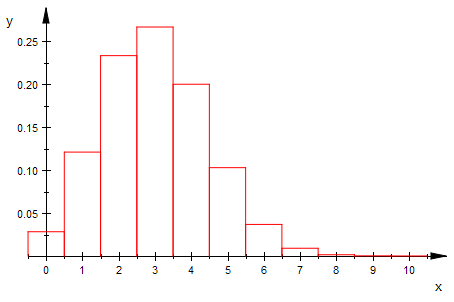
![]()
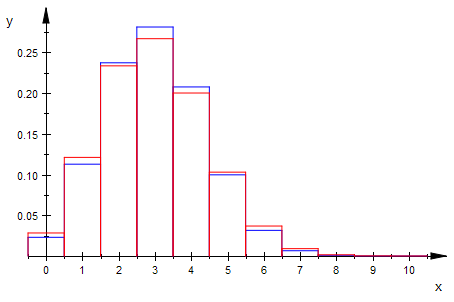
Will man beide Verteilungen vergleichen, muss man
hyHist(N,M,n,kmin,kmax,w) mit p=M/N, my=n M/N nehmen.
plot(histhy,histbi)
#########################################
Lotto, 6 aus 46
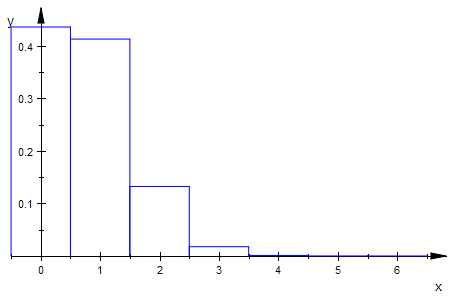
Deutlich ist die Lottoziehung ohne Zurücklegen.
M=6 Richtige sind da, n=6 werden gezogen.
hypHist(49,6,6,0,6,0);
![]()
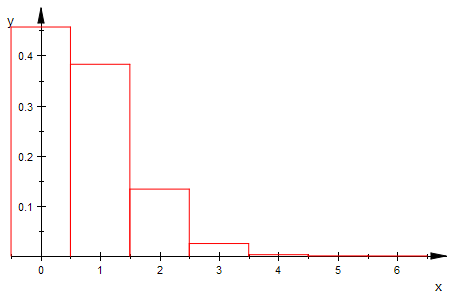
my=n*p und p=M/N, wenn man also die Lotto-Ziehung mit der Binomialverteilung
rechnen wollte, muss man sich offenbar vorstellen, dass die Wahrscheinlichkeit 6/49,
mit der man die erste Richtige zieht, nun auch für die anderen 5 Zahlen
zutrifft. Eigentlich ist es ja 5/48,....1/44.
biHist(6,6/49,0,6,0)
![]()
Der Erwatungswert stimmt exakt (per def) und sigma ist hier größer.
plot(histhy,histbi)
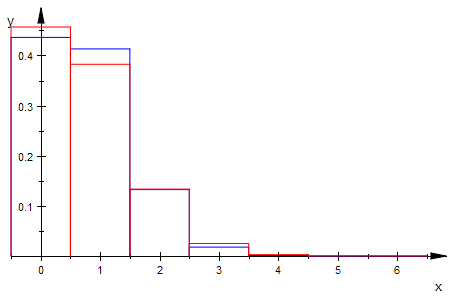
Die beiden Verteilungen verschränken sich interessant.
lotto:=binomial(49,6)
![]()
Für 6 Richtige
["binomial",(6/49.0)^6];
["elementar",1/lotto,1.0/lotto];
["hypergeo",binomial(6,6)*binomial(43,43)/binomial(49,6)];
["am Baum",6/49*5/48*4/47*3/46*2/45*1/44];
![]()
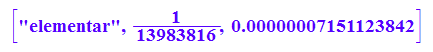
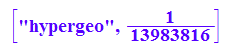
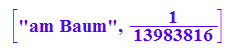
Biniomial bringt eine etwa 50-fach zu große Wahrscheinlichkeit für 6 Richtige.
(6/49.0)^6*lotto
![]()
plot(histhy,histbi,ViewingBoxYRange=0..0.000005)