[Algebra] [Lineare Algebra] [MuPAD]
| www.mathematik-verstehen.de | |||
[Algebra] [Lineare Algebra] [MuPAD] | |||
Hier wird eine Gerade als Funktion ihres Parameters definiert.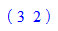
Zum Zeichnen nimmt man den Pfeil-Befehl.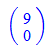
Eindrucksvolle annimierte Geradendarstellung: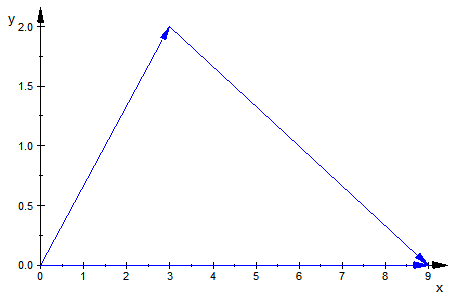

Zum Animieren: Doppeklick in der Graphik, dann oben Player bedienen.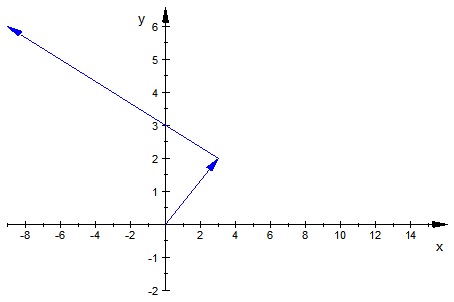

Herstellen der üblichen 2d-Geradengleichung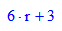
Hinten kann mann die Gleichung ablesen.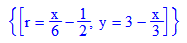
Zum Animieren: Doppeklick in der Graphik, dann oben Player bedienen.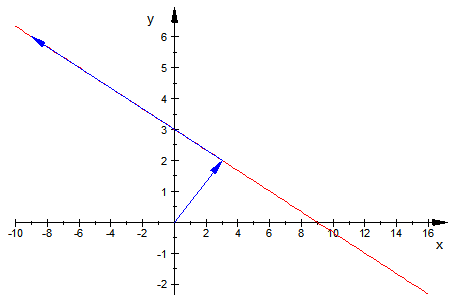

Hier wird eine Gerade als Funktion ihres Parameters definiert.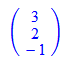
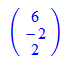
Zum Zeichnen nimmt man den Pfeil-Befehl.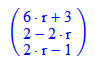
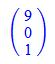
3D-Graphik "anfassen", d.h. Doppelkick in der Graphik, dann mit Maus drehen.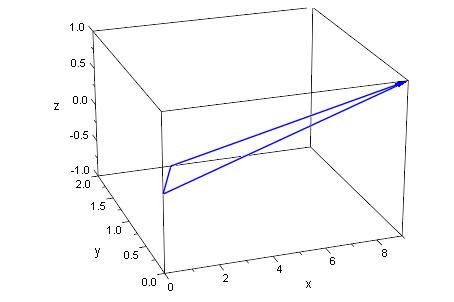

Beim Drehen der Graphik kann man nun schön die räumliche Anordnung sehen.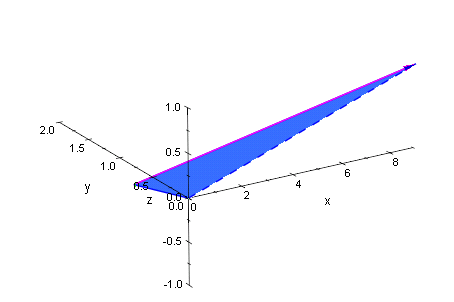

Das überrascht nicht. Die Geraden sind windschief.
Die Ebene und die Gerade schneiden sich.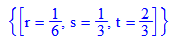
6. Mehrere Ebenen ###########################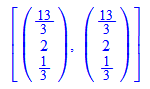
Bei drei Gleichungen für die 4 Parameter ist zu erwarten,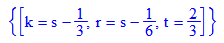
Orts und Richtungsvektor der Schnittgeraden sind: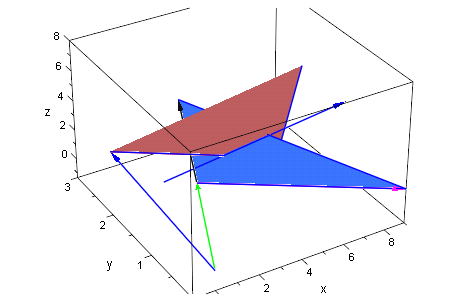

https://mathe.web.leuphana.de http://mathematik.uni-lueneburg.de |