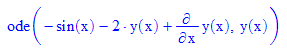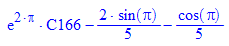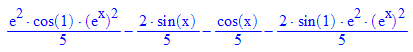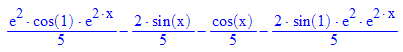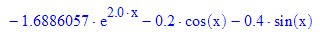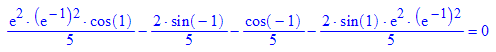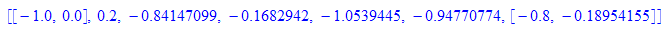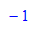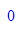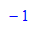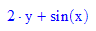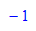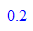URL [haftendorn.uni-lueneburg.de/mathe-lehramt] Differentialgleichungen
Mathematik mit MuPAD 3.11, Prof. Dr. Dörte Haftendorn ursprünglich 09.10.01
überarbeitet Sept. 05
Achtung: Menu ->Notebook->Evaluiere->Alle Eingaben

• dgl:=ode(y'(x)-2*y(x)=sin(x),y(x));//DGL eintragen

• solve(dgl)

• yallg:=op(solve(dgl));   

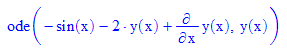
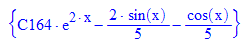
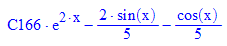
• yy:=x->yallg:yy(1)  //Funktion daraus machen:Dieses gelingt nicht. 

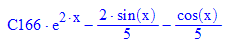
• yloesAllg:=xx->subs(yallg,x=xx): //Ohne diesen Klimmzug ging es nicht.

• yloesAllg(x)

• yloesAllg(PI)

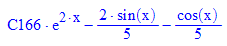
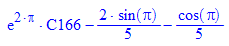
ode heißt ordinary differential equation, gewöhnliche Differentialgleichung, als Argument hat ode die eigentliche
Gleichung und die Funktion, die gesucht ist. solve kann die so gegebene Differentialgleichung allgemein lösen.
Anfangswertproblem

• x0Wert:=-1:y0Wert:=0://AWP  eintragen, x0, x0 sollen freie Variable bleiben

• dglAWP:=ode({y(x0Wert)=y0Wert,  y'(x)-2*y(x)=sin(x)  },y(x));//DGL eintragen

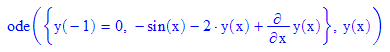
• loes:=xx->subs(op((solve(dglAWP))),x=xx):
  loes(x);simplify(loes(x));  float(simplify(loes(x)));

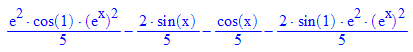
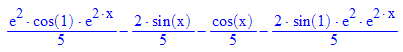
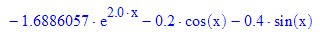
Proben für diese Lösung:

• loes'(x)-2*loes(x)  //linke Seite der DGL eintragen, rechts muss dann kommen

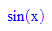
• loes(x0Wert)=y0Wert; float(loes(x0Wert))=y0Wert

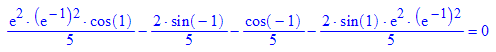
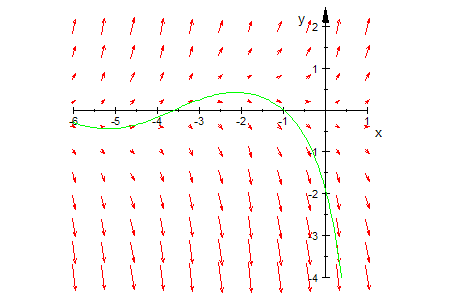
Zeichnen des Richtungsfeldes von DGLn 1. Ordnung,
die man nach y' auflösen kann

• g:=(x,y)->(2*y+sin(x)):g(x,y);//DGL eintragen!!!!!!! 

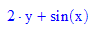
• xmin:=-6:xmax:=1:ymin:=-4:ymax:=2://Fenster eintragen !!!!!!!!!!!!

• loesGraph:=plot::Function2d(loes(x),x=xmin..xmax,ViewingBoxYRange=ymin..ymax,
  Color=RGB::Green):

• DIGITS:=5:
  field:= plot::VectorField2d( [1,g(x,y)], x=xmin..xmax,y=ymin..ymax,
     Color =  RGB::Red)://Die 1 musss sein!!!!!!

• plot(field,loesGraph, Scaling = Constrained)
  

Numerische Lösung entsprechend der Vorlesung Ha
Seite aus dem Vorlesungsskiptum hierzu
Heunverfahren

• heun:=proc(x0,y0) local x00,y00,m0,mz,z,mm,x1,y1;
  begin
  x00:=float(x0):y00:=float(y0):
  x1:=x00+h: m0:=g(x00,y00):z:=y00+m0*h:
  mz:=g(x1,z):mm:=(m0+mz)/2:y1:=y00+mm*h:
  return(x1,y1)
  end_proc:

• heunPrint:=proc(x0,y0,h) local x00,y00,m0,mz,z,mm,x1,y1;
  begin
  x00:=float(x0):y00:=float(y0):
  x1:=x00+h: m0:=g(x00,y00):z:=y00+m0*h:
  mz:=g(x1,z):mm:=(m0+mz)/2:y1:=y00+mm*h:
  DIGITS:=8;
  [[x00,y00],h,m0,z,mz,mm,[x1,y1]];
  end_proc:

• h:=0.2:heun(x0Wert,x0Wert)// Schrittweite wählen 

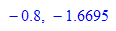
• heunPrint(x0Wert,y0Wert,h)

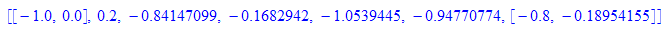
Hier stehen [x0,y0],h,m0,z,mz,mm,[x1,y1]

• heun(heun(x0Wert,y0Wert))  //Ein nächster Schritt

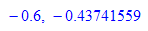
• heunPrint(heun(x0Wert,y0Wert),h)

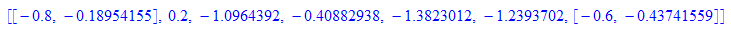
• n:=6:liste:=(heun@@i)(x0Wert,y0Wert) $ i=1..n://Folge xi,yi

• punkte:=[liste[j],liste[j+1]]$ j=1..2*n-1://Kombination zu Punkten

• punkte:=punkte[2*j-1] $ j=1..n //Folge der Heunpunkte

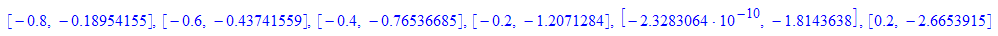
• punkte:=[x0Wert,y0Wert],punkte;  //Davor der Start zugefügt

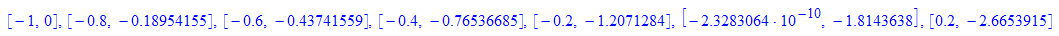
• heunpkte:=plot::Listplot([punkte],PointSize=2,Color=RGB::Green):
  plot(field,heunpkte)

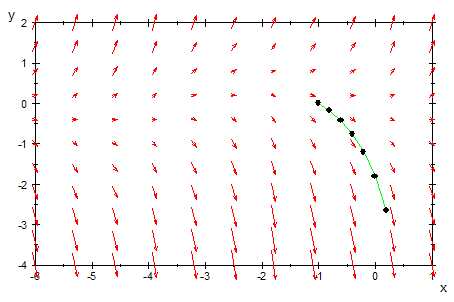
• plot(field,heunpkte,loesGraph,Axes=Origin,
  
  TicksDistance = 2.0, GridVisible = TRUE,
       SubgridVisible = TRUE,Scaling=Constrained)

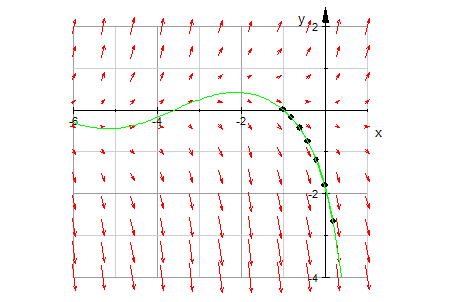
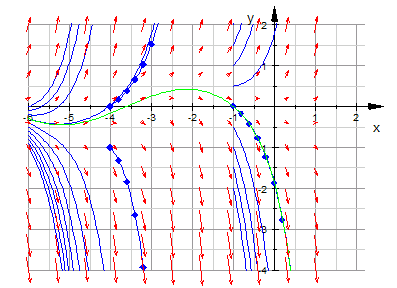
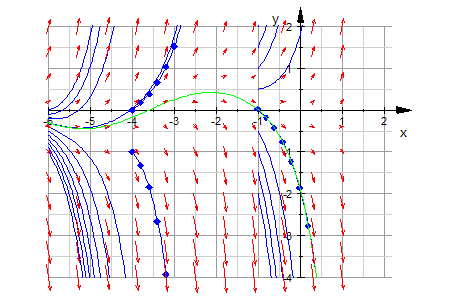
Die exakte Lösung stimmt mit der numerischen Lösung und dem Richtungsfeld gut überein.
Numerische Lösung mit MuPAD
Frage, welche Syntax odesolve hat und wie man DGLn zeichnet

• h:=0.2: n:=6: //Wie oben

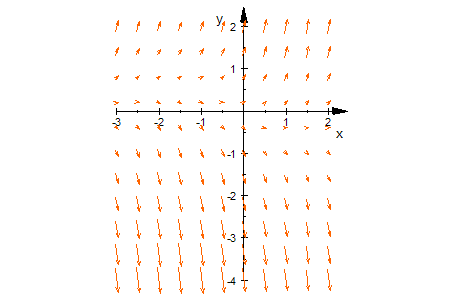
• Feld := plot::VectorField2d([1, g(x, y)], x = -3..2, y = -4..2,
   Color = RGB::Orange):plot(Feld, Scaling=Constrained)
  //Feld hat nur etwas andere Maße als field

• x0Wert;y0Wert;//zur Erinnerung

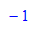
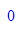
Hier muss man nochmal die DGL eintragen, denn in g(x,y) ist y nur als Variable.
Mit dem folgenden Befehl werden G, X0 und Y0 belegt.

• [G,X0, Y0] := [numeric::ode2vectorfield(
        {y'(x) = 2*y(x)+sin(x) , y(x0Wert) =y0Wert}, [y(x)])]

• X0

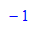
Erzeugung der Werte mit numeric::odesolve

• MuPkte:=[x0Wert+i*h,
        op(numeric::odesolve(
         G, X0..x0Wert+i*h, [0],Stepsize=h, RK4))]$i=1..n:

Stepsize=h, RK4))]$i=1..n:

Wichtig ist, dass man mit RK4 das Rung-Kutta-Verfahren 4.Ordnung wählt.
Alternative ist u.a. Euler1

• MuPkte:=[x0Wert,y0Wert],MuPkte

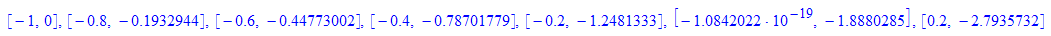
• MuPkteGraph:=plot::Listplot([MuPkte],
          PointSize=3,PointStyle=Stars,Color=RGB::Magenta):
  plot(Feld,MuPkteGraph,heunpkte, Axes=Origin, TicksDistance = 1, GridVisible = TRUE,
       SubgridVisible = TRUE):

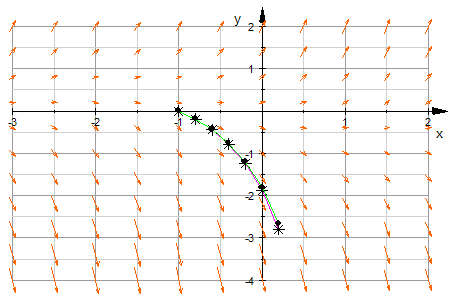
Man sieht, dass die Runge-Kutta-Punkte und die Heun-Punkte
fast aufeinander liegen.

• g(x,y);x0Wert;y0Wert;h; //zur Erinnerung

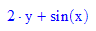
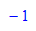
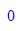
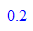
[G,X0, Y0] ist oben schon erzeugt
Hier wird nun die numerische Lösung direkt von Mupad gezeichnet.

• p1 := plot::Ode2d(G, [-1+i*h $ i=0..6], Y0,RK4,Stepsize=h,
                   PointSize = 2*unit::mm,
                   PointStyle = FilledCircles):
  

• p2:= plot::Ode2d(G, [-4+i*h $ i=0..6], Y0,RK4,Stepsize=h,
                   PointSize = 2*unit::mm,
                   PointStyle = FilledDiamonds):

• p3:= plot::Ode2d(G, [-4+i*h $ i=0..6], [-1],RK4,Stepsize=h,
                   PointSize = 2*unit::mm,
                   PointStyle = FilledDiamonds):

• plot(p1,p2,p3,loesGraph,field ,TicksDistance = 1, GridVisible = TRUE,
       SubgridVisible = TRUE,Scaling=Constrained):
  

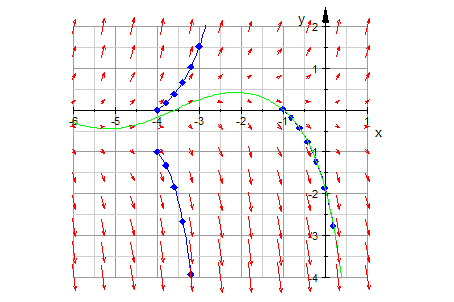
• all:=plot::Ode2d(G, [-6+i*h $ i=0..16], [-1+k*0.1],RK4,Stepsize=h,
                   PointsVisible =FALSE)$ k=0..10:
  all2:=plot::Ode2d(G, [-1+i*h $ i=0..16], [-2+k*0.5],RK4,Stepsize=h,
                   PointsVisible =FALSE)$ k=0..10:
  

• plot(all,all2,p1,p2,p3,loesGraph,field ,TicksDistance = 1, GridVisible = TRUE,
       SubgridVisible = TRUE,Scaling=Constrained)

Isoklinen Vorlesungsseite dazu

• iso:=(x,m)->op(solve(m=g(x,y),y)):iso(x,m);

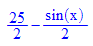
• alleIso:= iso(x,m/4) $ m=-8..8//Achtung, Bereich anpassen

• plotfunc2d(alleIso)

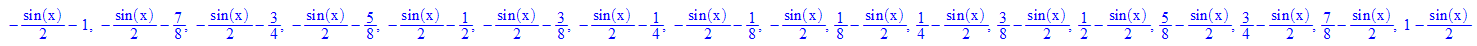
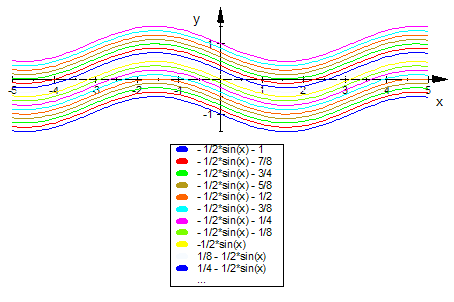
Man sieht hier deutlich, dass nur in einem schmalen Bereich um die x-Achse herum flache
Steigungen vorkommen können. In diesem Bereich entscheidet sich durch kleinste Änderungen
in den Anfangswerten, ob die Lösungsfunktion nach oben oder nach unten geht.

• alleIso:=plot::Function2d(iso(x,m/2),x=-6..xmax,
  Color=RGB::Green ) $ m=-8..8:

• plot(alleIso,field,Scaling = Constrained)

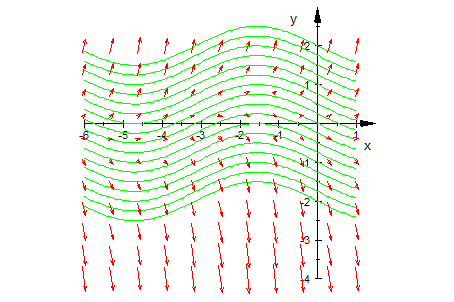
In diesem Bereich entscheidet sich durch kleinste Änderungen
in den Anfangswerten, ob die Lösungsfunktion nach oben oder nach unten geht. URL [haftendorn.uni-lueneburg.de/mathe-lehramt]