 URL [haftendorn.uni-lueneburg.de/mathe-lehramt]
Kurven von Vorder- und Hinterad beim Fahrrad.
URL [haftendorn.uni-lueneburg.de/mathe-lehramt]
Kurven von Vorder- und Hinterad beim Fahrrad.
Problemidee von Robert Jonsson, 2005 Jg. 12 Johanneum
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 3.9.05 Update 6.9.05
Web: haftendorn.uni-lueneburg.de/mathe-lehramt haftendorn.uni-lueneburg.de/ing-math
Achtung: Menu ->Notebook->Evaluiere->Alle Eingaben
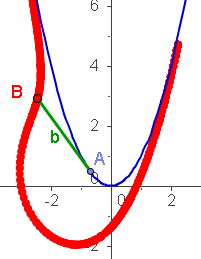
B ist das Vorderrad eines Fahrrades, A ist das Hinterrad.
Wenn B von rechts nach links auf der roten Kurve fährt,
dann fährt das Hinterrad auf der blauen Kurve. Das Fahrrad b
ist stets Tangente an die Hinterradkurve.
Diese GeoGebra-Konstruktion ist aber anders herum erzeugt.
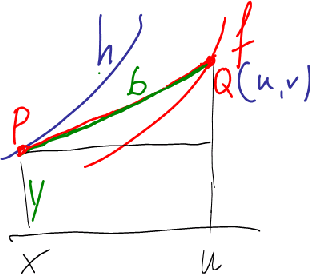
Nun also richtig herum: Q(u,v) läuft auf einer Kurve f und zieht
P(x,y) hinter sich her. Gesucht ist die Bahn h von P.
--------------------------------------------------------------------------
Gliederung:
1. Herleitung der DGL und einer Hilfsgleichung,
aus der bei kenntnis der Vorderradkurve noch u eliminiert werden muss.
2. Durchführung für den Spezialfall "f ist Gerade", das ergibt die gewöhnliche Traktrix.
Hierbei auch Richtungsfeld und Zeichung, konventionelle numerische Lösung der DGL.
3. Bei "f ist Kreis" ist stationären Fall auch h ein Kreis, Einleitungskurve theoretisch
unendlich kompliziert
4. Ganz neuer Ansatz (i.w. von Robert Jonsson) für eine direkte numerische Lösung.
Das gelingt (zunächst) für alle Bahnkurven, die als Funktion geschrieben sind.
--------------------------------------------------------------------------
1. Herleitung der DGL und einer Hilfsgleichung,
Es gilt: 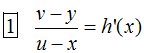 ,
, 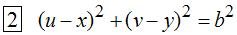 ,
,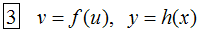 Informationen in Gleichung 2 zusammengeführt ergibt
Informationen in Gleichung 2 zusammengeführt ergibt 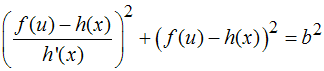
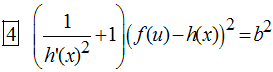
Für jeder Vorderradkurve f ist u zu eliminieren aus 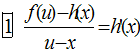
und dann in Gleichung 4 zu verwenden. Gleichung 4 ist dann eine Differentialgleichung
für die Funktion h.
--------------------------------------------------------------
2. Spezialfall 1: gewöhnliche Traktrix, 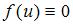
- solve((1/k^2+1)*t^2=b^2,k)
- assume(b,Type::Real);assume(b>0)

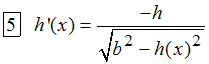
ist die zu lösende Differentialgleichung, die positive Lösung
passte nicht zum Problem
- g:=(x,y)->-y/sqrt(b^2-y^2)
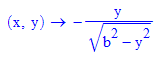
- xmin:=-2:xmax:=4:ymin:=-1:ymax:=5:
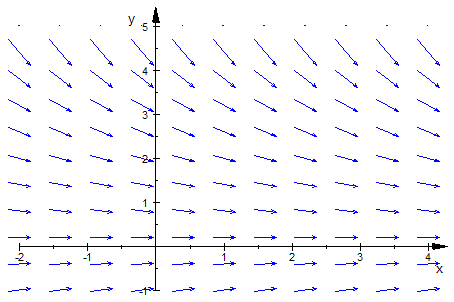
- richtungsfeld:= plot::VectorField2d( [1,g(x,y)], x=xmin..xmax,y=ymin..ymax,
Color = RGB::Blue)://Die 1 musss sein!!!!!!

- dgl:=ode(y'(x)= -y(x)/sqrt(b^2-y(x)^2) ,y(x))
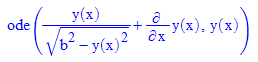
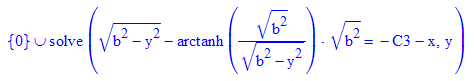
Was hier mit y bezeichnet ist, ist die gesuchte Funktion h,
leider aber müsste man nach y auflösen. Das aber geht nicht, da es sich um eine
transzendente Gleichung handelt. Zusaätzlich ist der arctanh nur für Argumente
betragsmäßig kleiner 1 definiert, hier aber ist das Argument größer 1.
- x0Wert:=0:y0Wert:=4:b:=4:n:=20:delta:=0.2:
- [G,X0, Y0] := [numeric::ode2vectorfield(
{y'(x) = -y(x)/sqrt(b^2-y(x)^2) , y(x0Wert) =y0Wert}, [y(x)])]:
- MuPkte:=[x0Wert+i*delta,
op(numeric::odesolve(
G, X0..x0Wert+i*delta, [3.9],Stepsize=delta, RK4))]$i=1..n:
- MuPkteGraph:=plot::Listplot([MuPkte],
PointSize=3,PointStyle=Stars,Color=RGB::Magenta):
- plot(richtungsfeld,MuPkteGraph, Axes=Origin, TicksDistance = 1, GridVisible = TRUE,
SubgridVisible = TRUE,Scaling=Constrained)
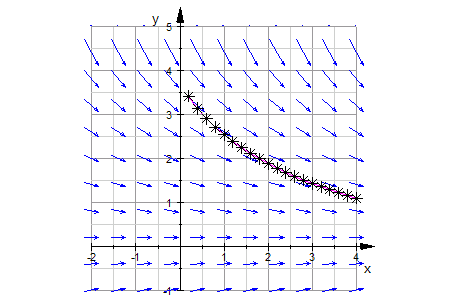

3. Spezialfall 2 Vorderradkurve ist ein Kreis mit Radius R.
Dann ist als Gleichgewicht für das Hinterrad auch ein
Kreis mir Radius r zu erwarten. Es gilt: 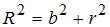
Wenn man aber aus der Geradeausfahrt in den Kreis einbiegt
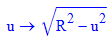
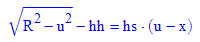
- assume(hh,Type::Real):assume(hs,Type::Real):
assume(x,Type::Real):assume(R>0)
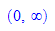
- //solve((f(u)-hh)=hs*(u-x),u) // unmöglich
+++++++++++++++++++++++++++++++++++++++++++++
4. Numerisch aus direktem Ansatz
bekannt sein müssen: f, die Vorderradfunktion,
eine Startsituation und die Schrittweite du.
Neue Idee, wie sie Robert eigentlich schon längst hatte.
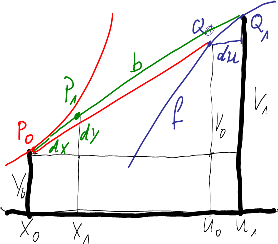
Start mit 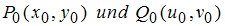 .
. 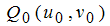 rückt auf der Kurve f
rückt auf der Kurve f
nach 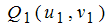 .Nun wird die Verbindungsgerade
.Nun wird die Verbindungsgerade 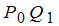 als Tangente
als Tangente
an die gesuchte Kurve aufgefasst und auf ihr von Q aus die Fahrradlänge b abgetragen.
Dann braucht nur noch iteriert zu werden.
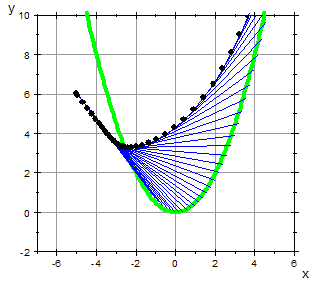
- du:=0.2:b:=5:x0:=-5:y0:=6:n:=50:f:=x->1/2*x^2;
u0:=-2:v0:=2:
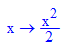
- fkt:=plot::Function2d(f(x),Color=RGB::Green, LineWidth=1):
- fahrr:=proc(x0,y0,u0,v0,m0,du)
local delta,x1,y1,u1,v1,m1;
begin
u1:=u0+du: v1:=f(u0):
m1:=(v1-y0)/(u1-x0):
x1:=-b/sqrt(1+m1^2)+u1: //etwas Strahlensätze
y1:=m1*(x1-x0)+y0:
return(x1,y1,u1,v1,m1,du):
end_proc:
- mat:=matrix([[i,(fahrr@@i)(x0,y0,u0,v0,m0,du)] $i=1..n])://Iteration
- alle:=[x0,y0],[mat[i,2],mat[i,3]]$i=1..n: //Punktliste
- stangen:=plot::Line2d([mat[i,2],mat[i,3]],[mat[i,4],mat[i,5]])$i=1..n:
li:=plot::Listplot([alle], PointSize=2):plot(fkt,stangen,li,
Scaling=Constrained,GridVisible=TRUE, ViewingBox=[-7..6,-2..10]):
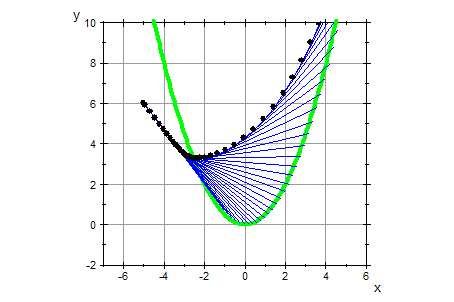
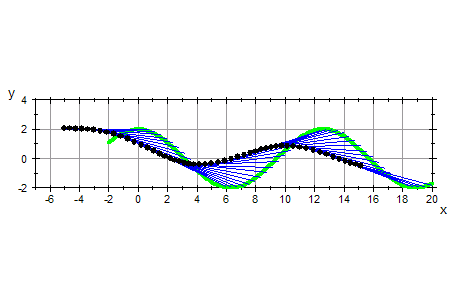
Anderes Beispiel
- du:=0.2:b:=5:x0:=-5:y0:=6:n:=30:f:=x->sqrt(36-x^2);
u0:=-0:v0:=6:
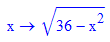
- fkt:=plot::Function2d(f(x),Color=RGB::Green, LineWidth=1):
fahrr:=proc(x0,y0,u0,v0,m0,du)
local delta,x1,y1,u1,v1,m1;
begin
u1:=u0+du:v1:=f(u0):
m1:=(v1-y0)/(u1-x0):
x1:=-b/sqrt(1+m1^2)+u1:
y1:=m1*(x1-x0)+y0:
return(x1,y1,u1,v1,m1,du):
end_proc:
mat:=matrix([[i,(fahrr@@i)(x0,y0,u0,v0,m0,du)] $i=1..n]):
- alle:=[x0,y0],[mat[i,2],mat[i,3]]$i=1..n:
- stangen:=plot::Line2d([mat[i,2],mat[i,3]],[mat[i,4],mat[i,5]])$i=1..n:
li:=plot::Listplot([alle], PointSize=2):plot(fkt,stangen,li,
Scaling=Constrained,GridVisible=TRUE, ViewingBox=[-7..6,-2..10]):
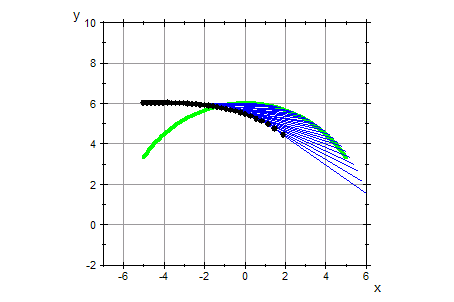
Weiteres Beispiel
- du:=0.4:b:=5:x0:=-5:y0:=2:n:=50:f:=x->2*cos(x/2);
u0:=0:v0:=2:
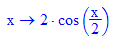
- fkt:=plot::Function2d(f(x),x=-2..20,Color=RGB::Green, LineWidth=1):
fahrr:=proc(x0,y0,u0,v0,m0,du)
local delta,x1,y1,u1,v1,m1;
begin
u1:=u0+du:v1:=f(u0):
m1:=(v1-y0)/(u1-x0):
x1:=-b/sqrt(1+m1^2)+u1:
y1:=m1*(x1-x0)+y0:
return(x1,y1,u1,v1,m1,du):
end_proc:
mat:=matrix([[i,(fahrr@@i)(x0,y0,u0,v0,m0,du)] $i=1..n]):
alle:=[x0,y0],[mat[i,2],mat[i,3]]$i=1..n:
stangen:=plot::Line2d([mat[i,2],mat[i,3]],[mat[i,4],mat[i,5]])$i=1..n:
li:=plot::Listplot([alle], PointSize=2):plot(fkt,stangen,li,
Scaling=Constrained,GridVisible=TRUE, ViewingBox=[-7..20,-2..4]):
 URL [haftendorn.uni-lueneburg.de/mathe-lehramt]
URL [haftendorn.uni-lueneburg.de/mathe-lehramt]
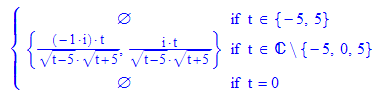


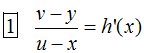 ,
, 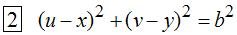 ,
,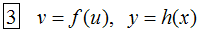 Informationen in Gleichung 2 zusammengeführt ergibt
Informationen in Gleichung 2 zusammengeführt ergibt 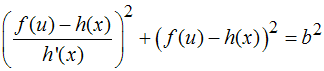
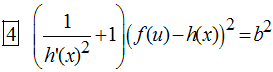
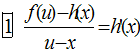
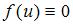
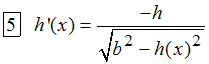
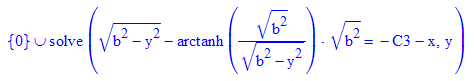
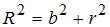


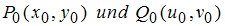 .
. 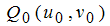 rückt auf der Kurve f
rückt auf der Kurve f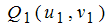 .Nun wird die Verbindungsgerade
.Nun wird die Verbindungsgerade 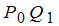 als Tangente
als Tangente
