URL [haftendorn.uni-lueneburg.de/mathe-lehramt]

Steinwurf mit Flatterband, Brücke mit Lampen

Idee Jörg Meyer, Hameln 10/99, Aufgegriffen Hellberg 02/01,
Durchführung: Dörte Haftendorn 02/01

download Mathematica-Notebook

x[t_] := t - L/(1 + 4t^2 )^(1/2) ; y[t_] := -t^2 - (-2L t)/(1 + 4t^2 )^(1/2) ;

Herleitung unten

Needs["Graphics`master`"]

L = 4 ;

RowBox[{RowBox[{bänder, =, RowBox[{Table, [, RowBox[{Line[{{t, -t^2}, {x[t], y[t]}}], ,, RowBo ... r />, ,, PlotRange {{-4, 3}, {-6, 3}}, ,, AspectRatio->Automatic}], ]}], ;}], <br />}]

[Graphics:index_5.gif]

RowBox[{RowBox[{RowBox[{L = 4, ;, RowBox[{bänder, =, RowBox[{Table, [, RowBox[{Line[{{t, -t^2} ... änder}, AspectRatio->Automatic] ;}], (*Animimieren D - Zelle Strg y    *)}]

[Graphics:index_7.gif]

RowBox[{Do, [, RowBox[{RowBox[{RowBox[{bänder, =, RowBox[{Table, [, RowBox[{Line[{{t, -t^2}, { ... ic}], ]}]}], ,, <br />,     , {L, .5, 5, .25}}], ]}]     

ParametricPlot[{{t - 4/(1 + 4 t^2)^(1/2), -t^2 + (8t)/(1 + 4 t^2)^(1/2)}, {t, -2t^2}}, {t, -2, 3}, AspectRatioAutomatic, PlotRange {-6, 3}] ;

[Graphics:index_30.gif]

Herleitung  ⇑

L=. ; x=. ; y=. ; u=. ; v=. ; t=.

Länge = ( (x - u)^2 + (y - v)^2L^2) ; Richtung = ((y - v)/(x - u)  -2t) ;

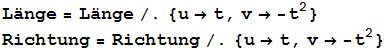
Länge = Länge/.{ut, v -t^2} Richtung = Richtung/.{ut, v -t^2}

(-t + x)^2 + (t^2 + y)^2 == L^2

(t^2 + y)/(-t + x) == -2 t

Solve[{Länge, Richtung}, {x, y}]//Simplify ;

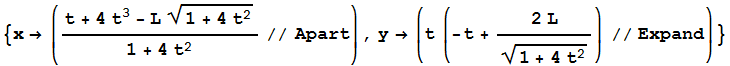
{x ((t + 4 t^3 - L (1 + 4 t^2)^(1/2))/(1 + 4 t^2)//Apart), y (t (-t + (2 L)/(1 + 4 t^2)^(1/2))//Expand)}

{xt - L/(1 + 4 t^2)^(1/2), y -t^2 + (2 L t)/(1 + 4 t^2)^(1/2)}

Created by Mathematica  (September 6, 2005)

URL [haftendorn.uni-lueneburg.de/mathe-lehramt]