	Johanneum Lüneburg	Dr. Dörte Haftendorn
	Informationssystem
	Fächer Mathematik Graphen AniGra

Das Heron-Verfahren

Näherungsweise Bestimmung von Quadratwurzeln und höheren Wurzeln.

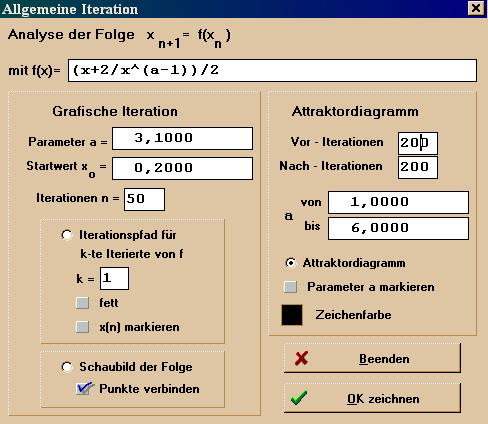Zeigen Sie, dass diese Folge gegen k-te Wurzel aus r konvergiert, wenn k größer als 1 nicht größer als 4 ist.

Als Erkundung mit Turboplot:

Wählen Sie "Iteration".
Tragen Sie die Trägerfunktion ein.
Die 2 im Zähler repräsentiert r=2 .
Experimentieren Sie mit verschiedenen r und a.
"Attraktordiagramm" heißt auch Feigenbaum-Diagramm.

Die Trägerfunktion selbst heißt "erste Iterierte". Sehen Sie sich an unter welchen Winkeln die zweiten Iterierten für a=4,5 die Wh schneiden. Wie hängt die Beobachtung mit dem Attraktordiagramm zusammen?

Sehen Sie sich auch das "Schaubild der Folge" an.

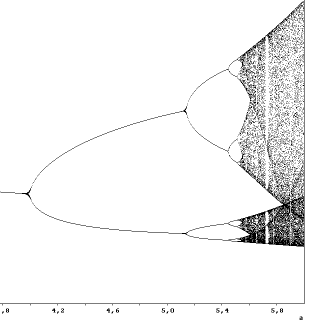Das eigentliche Heronverfahren berechnet Quadratwurzeln und hat obige Formel mit a=2.
Es konvergiert superschnell (d.h. die Trägerfkt. schneidet die Wh. mit Steigung 0.) und entspricht genau dem Newtonverfahren.
Den Tipp, hie höhere Wurzeln mit Herons Grundidee zu betrachten verdanke ich Hans Schneebeli (Schweiz).
Leicht kann man nachrechnen, das mit wachsendem a die Konvergenz schlechter wird und hinter a=a aufhört.

Das brauchte mich auf die Vermutung, dass nun eigentlich eine Bifurkationskaskade einsetzen müsste.

Tatsäch ist das so, ich hatte das zuerst 2001 in Mathematica realisiert.

Um Größernordnungen leichter sind die Betrachtungen aber mit Turboplot, so dass sie nun in die Reichweite von Schule rücken.
Nun kann geforscht werden!!!!!!!!!!!!!!!!!!!!!!!!

Autor: © [Prof. Dr. Dörte Haftendorn] Datum März 2002. Letzte Änderung am 09. Juni 2011
[Fächer] [Mathematik][Graphen][AniGra] [Mathe-Buch] [Webteam] [Email s.Ueberblick]