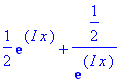
Besondere Maple Befehle
Überblick Prof. Dr. Dörte Haftendorn, Aug 2001
Umwandlungen
Convert allgemein
> convert(cos(x),exp);
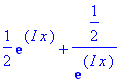
> convert(cosh(x),exp);
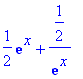
> factor(convert(cosh(x),exp));
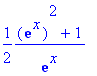
> ifactor(convert(cosh(x),exp));
Error, (in ifactor) invalid arguments
> sin(7 / 60 * Pi);
> convert(%,'radical');
![]()
![]()
>
>
Matrizen
> A:=<<1 | 2> , <3 | 9>>;
![A := _rtable[4547360]](gifbesonder/besondermaplebefehle6.gif)
Das war von der Palette
>
![]()
Merkwürdigerweise wird das hier nicht akzeptiert.
> A;
![_rtable[4450864]](gifbesonder/besondermaplebefehle8.gif)
> a;
![]()
> type(A,Matrix);
![]()
> convert(A,'listlist');
![]()
> A;
![_rtable[4450864]](gifbesonder/besondermaplebefehle12.gif)
> type(A,Matrix);
![]()
Also bleibt A selbst unberührt.
> Aset:=convert(A,set);
![]()
> Ali:=convert(Aset,'list');
> type(Ali,set);type(Aset,set);type(Ali,list);
![]()
![]()
![]()
![]()
> A;
![_rtable[4450864]](gifbesonder/besondermaplebefehle19.gif)
> convert(A,listlist);
![]()
>
>
izen
Vereinfachungen
> trigsum:=expand(sin(alpha+beta));
![]()
> combine(trigsum,trg);
![]()
> bruch:=(x^2-25)/(x+5);
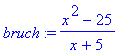
> normal(bruch);
![]()
> normal(bruch^(-3));
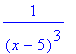
> convert(bruch^(-3)*(x^2-4),parfrac,x);
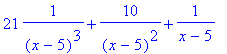
Das war Partialbruchzerlegung
> term:=(x^r)^2;
![]()
> combine(term,power);
![]()
> assume(r>0);assume(x>0);(x^r)^(1/r);
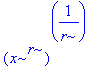
> combine(%,power);
![]()
Ohne die Festlegung von sinnvollen Bereichen von x und r kann es nicht klappen.
> x:='x':r:='r';
![]()
So hebt man die Einschränkungen für r und x wieder auf.
Auswerten
Die großgeschriebenen Funktionsnamen bedeuten inert fuction, d.h. inaktive Funktion.
Sie noch nicht ausgeführt sondern nur als Operator vorgesehen.
> F := Int(x, x);
![]()
> value(F);
![]()
>