Mathematik Verstehen Dörte Haftendorn: Abakus, Geschichte der Mathematik

Geschichte der Mathematik Leitseite URL haftendorn.uni-lueneburg.de/mathe-lehramt/geschichte/geschichte.htm © Prof. Dr. Dörte Haftendorn

	Abakus Interaktiver Abakus (Cindrella-Applet) Schon die Römer kannten den Abakus und er wird auch heute noch in Asien benutzt. Was ist das Geheimnis dieses Jahrtausende währenden Gebrauchs?
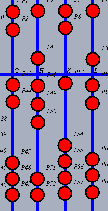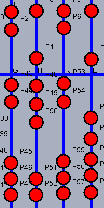
	Beim Abakus zählen die Kugeln, die an die Querstange geschoben sind. Die oberen zählen 5 und die unteren 1. Die Stangen entsprechen dem Stellenwertsystem, d.h. die Kugeln auf einer Stange zählen das 10-fache der Kugeln auf der Stange rechts daneben. Links ist also 2817 dargestellt. Der Abakus wird nur mit drei Fingern der rechten Hand bedient. Der Daumen schiebt Kugeln hoch, der Zeigefinger bedient die Fünferkugeln und der Mittelfinger schiebt Einserkugeln nach unten. Für die Rechnung plus 8 ist also hier nur die Drehbewegung "+10 -2 " nötig. Rechts ist demnach 2825 dargestellt. Ein geübter Abakusrechner macht das "nach Sicht". Er rechnet bei der Addition (und Subtraktion) nicht im Kopf. Man könnte den Abakus einen "Muskelkraft-betriebenen Kleincomputer" nennen. Siehe auch das Fazit nach der Multiplikation mit dem Abakus!

Multiplikand 2817 mal Multiplikator 623 = Produkt
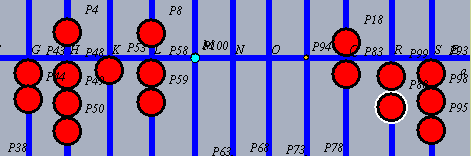	Multiplikation Der Multiplikand wird vorne eingestellt, der Mutiplikator hinten, nur zum Merken.
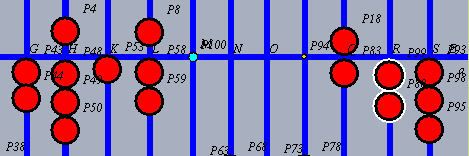	Die letzte Stelle des Multiplikanden, hier 7, wird mit der 2. Stelle des Multiplikators, hier 2, multipliziert.
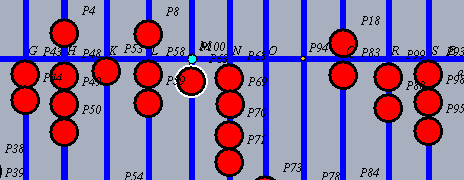	Das Ergebnis, hier 14, wird 2 Stellen rechts vom Multiplikanden eingestellt.

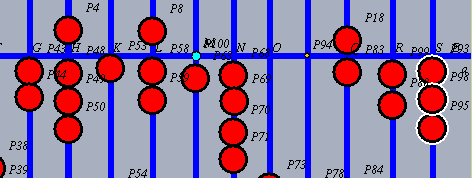	Die letzte Stelle des Multiplikanden, hier 7, wird mit der 3. Stelle des Multiplikators, hier 3, multipliziert.
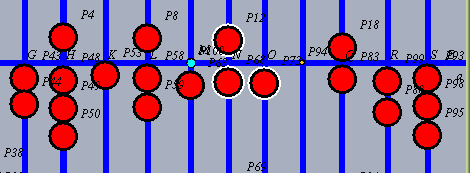	Das Ergebnis, hier 21, wird 3 Stellen rechts vom Multiplikanden addiert. Hier wird also die 2 zu der 4 addiert.
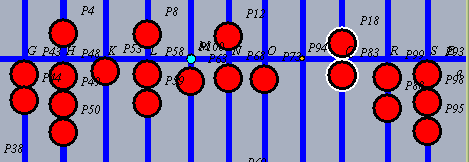	Hätte der Multiplikator noch mehr Stellen rechts, kämen nun erst diese alle dran. Schließlich: Die letzte Stelle des Multiplikanden, hier 7, wird mit der 1. Stelle des Multiplikators, hier 6, multipliziert.
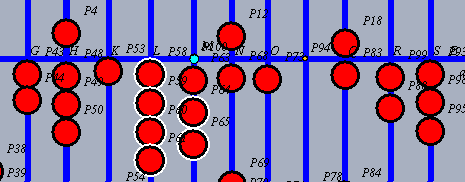	Nun hat die letzte Stelle des Multiplikanden, hier 7, ausgedient und wird abgeräumt.!!!!!!! Das Ergebnis, hier 42, wird auf die Stelle rechts daneben addiert, der Übertrag, hier 4, kommt auf den leergeräumten Platz. Der 1. Schritt ist fertig.
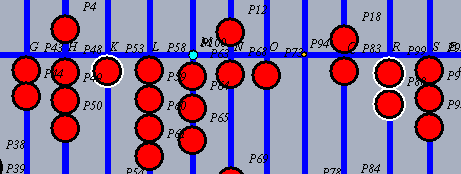	Nun wird für die vorletzte Stelle des Multiplikanden, hier 1, derselbe Algorithmus durchgezogen. Die nunmehr letzte Stelle des Multiplikanden, hier 1, wird mit der 2. Stelle des Multiplikators, hier 2, multipliziert.
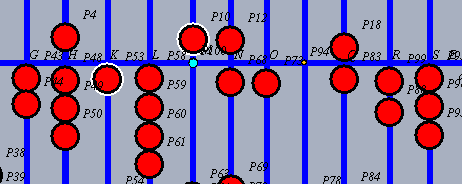	Das Ergebnis, hier 2, wird 2 Stellen rechts vom jetzigen Multiplikanden addiert. Hier wird also die 2 zu der 3 addiert. Das ergibt 5. Man kann sich Fälle Denken, bei denen Überträge weiter nach links "durchschlagen". Dann muss man man wohl weiter auseinander gerückt anfangen oder den Multiplikanden schriftlich notiert haben.
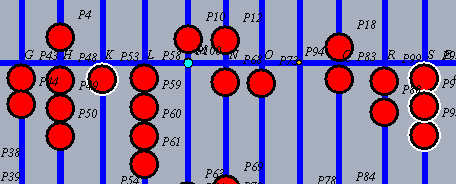	Die nunmehr letzte Stelle des Multiplikanden, hier 1, wird mit der 3. Stelle des Multiplikators, hier 3, multipliziert.
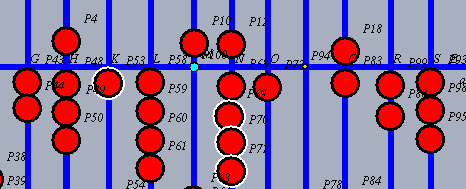	Das Ergebnis, hier 3, wird 3 Stellen rechts vom jetzigen Multiplikanden addiert. Hier wird also die 3 zu der 6 addiert.
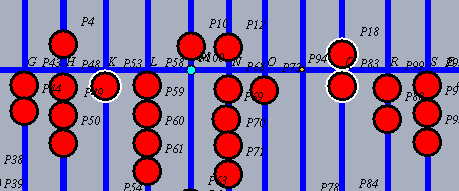	Hätte der Multiplikator noch mehr Stellen rechts, kämen nun erst diese alle dran. Schließlich: Die nunmehr letzte Stelle des Multiplikanden, hier 1, wird mit der 1. Stelle des Multiplikators, hier 6, multipliziert.
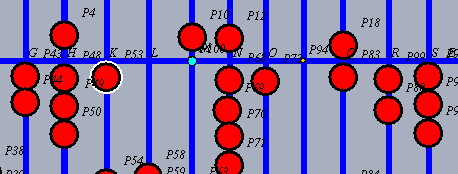	Nun hat die nunmehr letzte Stelle des Multiplikanden, hier 1, ausgedient und wird abgeräumt.!!!!!!! Das Ergebnis, hier 6, wird auf die Stelle rechts daneben addiert, da sind schon 4, ergibt dort 0 , der Übertrag, hier 1, kommt auf den leergeräumten Platz. Der 2. Schritt ist fertig.

	Nun wird für die vorvorletzte Stelle des Multiplikanden, hier 8, derselbe Algorithmus durchgezogen. Die nunmehr letzte Stelle des Multiplikanden, hier 8, wird mit der 2. Stelle des Multiplikators, hier 2, multipliziert.
	Das Ergebnis, hier 16, wird 2 Stellen rechts vom jetzigen Multiplikanden addiert. Hier wird also die 6 zu der 0 addiert, und die 1 zur 1, ergibt 2
	Die nunmehr letzte Stelle des Multiplikanden, hier 8, wird mit der 3. Stelle des Multiplikators, hier 3, multipliziert. Das Ergebnis, hier 24, wird 3 Stellen rechts vom jetzigen Multiplikanden addiert. Hier wird also die 4 zu der 5 addiert und die 2 zur 6
	Hätte der Multiplikator noch mehr Stellen rechts, kämen nun erst diese alle dran. Schließlich: Die nunmehr letzte Stelle des Multiplikanden, hier 8, wird mit der 1. Stelle des Multiplikators, hier 6, multipliziert.
	Nun hat die nunmehr letzte Stelle des Multiplikanden, hier 8, ausgedient und wird abgeräumt.!!!!!!! Das Ergebnis, hier 48, wird auf die Stelle rechts daneben addiert, da sind schon 2, ergibt dort 0 , der Übertrag, hier 5, kommt auf den leergeräumten Platz. Der 3. Schritt ist fertig.
	Die nunmehr letzte Stelle des Multiplikanden, hier 2, wird mit der 2. Stelle des Multiplikators, hier 2, multipliziert.
	Das Ergebnis, hier 4, wird 2 Stellen rechts vom jetzigen Multiplikanden addiert. Hier wird also die 4 zu der 0 addiert,
	Die nunmehr letzte Stelle des Multiplikanden, hier 2, wird mit der 3. Stelle des Multiplikators, hier 3, multipliziert.
	Das Ergebnis, hier 6, wird 3 Stellen rechts vom jetzigen Multiplikanden addiert. Hier wird also die 6 zu der 8 addiert, macht 4 und 1 übertrag, der auf der Nachbarstange zu 5 füht.
	Hätte der Multiplikator noch mehr Stellen rechts, kämen nun erst diese alle dran. Schließlich: Die nunmehr letzte Stelle des Multiplikanden, hier 2, wird mit der 1. Stelle des Multiplikators, hier 6, multipliziert. Nun hat die nunmehr letzte Stelle des Multiplikanden, hier 2, ausgedient und wird abgeräumt.!!!!!!! Das Ergebnis, hier 12, wird auf die Stelle rechts daneben addiert, der Übertrag, hier 5, kommt auf den leergeräumten Platz. Der 4. Schritt ist fertig.
	Das Ergebnis 1754991 steht im Abakus. 2817 mal 623 = 1754991 Fazit: Man braucht nur das kleine Einmaleins und sonst keine Kopfrechungen, "nur" einen guten Blick und drei schnelle Finger für Additionen.

[Geschichte] Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn

Sept. 2003, update 10. Oktober 2011

Internetadressen dieses Web-Verbundes [www.doerte-haftendorn.de] [haftendorn.uni-lueneburg.de/mathe-lehramt] [haftendorn.uni-lueneburg.de/ing-math]