Kegelschnitte aus der Kreisabstandskonstruktion

	Herr Zvonimir Durcevic sandte mir aus Wien einen weiteren Brief mit wunderschönen Handzeichnungen für eine Variante der gemeinsamen Leitkreiskonstruktion der Kegelschnitte. Diese sind im Folgenden dargestellt.
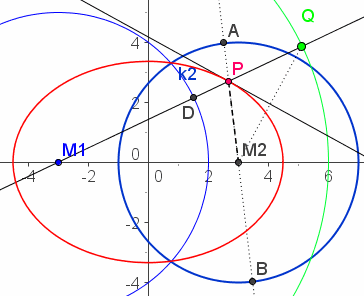Der geometrische Ort aller Punkte, die von zwei festen Kreisen denselben Abstand haben		interaktive Datei mit Geogebra download
Erklärung	Gegeben sind zwei Kreise mit den Radien r1 und r2. Um den Mittelpunkt M1 wird ein Kreis mit dem Radius r3=r1+r2 geschlagen.Q wandert auf diesem Kreis, P ergibt sich mit der Mittelsenkrechten wie bei der Leitkreiskonstruktion. Ersichtlich hat P von beiden Kreisen denselben Abstand. Denn: DQ=r2 per Konstruktion. aber auch AM2=r2. Da P auf der Mittelsenkrechten von QM2 liegt, ist PQ=PM2 und damit DP=PA. Es handelt sich also um eine Uminterpretation der Leitkreiskonstruktion. Der Radius des Leitkreises kann in beliebiger Weise in zwei Kreisradien aufgeteilt werden. Es ist aber sehr hübsch, dass sich auch alle Besonderheiten der Leitkreiskonstruktion wieder ergeben. Insbesondere entstehen Hyperbeln, wenn die beiden Ausgangskreise sich nicht mehr schneiden. Man kann das in der GeoGebra-Datei selbst erkunden.

[Kurven]
Inhalt:Zvonimir Durcevic undHaftendorn Web: Prof. Dr. Dörte Haftendorn

Juli 05, update 18. April 2008