 URL [haftendorn.uni-lueneburg.de/mathe-lehramt]
URL [haftendorn.uni-lueneburg.de/mathe-lehramt]
Traktix-Varianten mit DGLn
Prof. Dr. Dörte Haftendorn, Universität Lüneburg, Mai 2004
•Vorstellung: Q bewegt sich an der Tischkante und zieht einen Punkt P aus dem Ursprung weg so, dass PQ Normale der Bahnkurve ist und ![Overscript[PQ, _]](traktrix-b/traktrix-dgl-variante1_1.gif) die feste Länge k hat.
die feste Länge k hat.
•DGL
•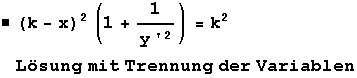
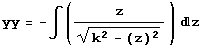
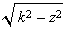
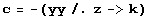
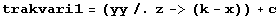
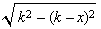
![t1 = Plot[trakvari1 /. k -> 4, {x, 0, 8}, PlotRange -> {0, 4}, PlotStyle -> Farbig] ;](traktrix-b/traktrix-dgl-variante1_9.gif)
![[Graphics:traktrix-b/traktrix-dgl-variante1_10.gif]](traktrix-b/traktrix-dgl-variante1_10.gif)
•Parameterdarstellung, t Steigungswinkel der Uhrkette
•![k - x == Cos[t] ; y ' == -1/Tan[t]](traktrix-b/traktrix-dgl-variante1_11.gif)
•Mit 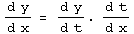 folgt
folgt ![(d y)/(d t) == k Cos[t]](traktrix-b/traktrix-dgl-variante1_13.gif)
•Trennung der Variablen:
![k ∫ Cos[t] d t](traktrix-b/traktrix-dgl-variante1_14.gif)
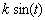
![y[t_] := k Sin[t]](traktrix-b/traktrix-dgl-variante1_16.gif)
![x[t_] := k (1 - Cos[t])](traktrix-b/traktrix-dgl-variante1_17.gif)
•Parameterdarstellung der Traktrix-Variante 1
![t2 = ParametricPlot[{x[t], y[t]} /. k -> 4, {t, 0, 3}, PlotRange -> {0, 4}, AspectRatio -> Automatic] ;](traktrix-b/traktrix-dgl-variante1_18.gif)
![[Graphics:traktrix-b/traktrix-dgl-variante1_19.gif]](traktrix-b/traktrix-dgl-variante1_19.gif)
![Show[t1, t2, AspectRatio -> Automatic] (* es ist wirklich derselbe Graph, und zwar der Kreis *)](traktrix-b/traktrix-dgl-variante1_20.gif)
![[Graphics:traktrix-b/traktrix-dgl-variante1_21.gif]](traktrix-b/traktrix-dgl-variante1_21.gif)
Converted by Mathematica
(May 16, 2004)
 URL [haftendorn.uni-lueneburg.de/mathe-lehramt]
URL [haftendorn.uni-lueneburg.de/mathe-lehramt]
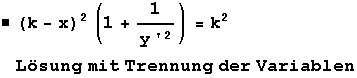
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:traktrix-b/traktrix-dgl-variante1_10.gif]](traktrix-b/traktrix-dgl-variante1_10.gif)
![k - x == Cos[t] ; y ' == -1/Tan[t]](traktrix-b/traktrix-dgl-variante1_11.gif)
![]()
![]()
![]()
![]()
![]()
![[Graphics:traktrix-b/traktrix-dgl-variante1_19.gif]](traktrix-b/traktrix-dgl-variante1_19.gif)
![]()
![[Graphics:traktrix-b/traktrix-dgl-variante1_21.gif]](traktrix-b/traktrix-dgl-variante1_21.gif)
![]()