Stochastik Leitseite URL haftendorn.uni-lueneburg.de/mathe-lehramt/stochastik/stochastik.htm       © Prof. Dr. Dörte Haftendorn

Markow-Ketten mit zwei Zuständen
Stochastik mit MuPAD,
Prof. Dr. Dörte Haftendorn 15.11.04 Version vom 15.11.04
-----------------------------------------------------------------------------------

Zwei Zustände:
ja, die Handwerker sind heute da
nein: die Handwerker sind heute nicht da
Die Prozentsätze geben an, mit welcher Wahrscheinlichkeit morgen der
betreffende Zustand eintritt.
Also: Wenn heute Handwerker da sind, sind sie mit 70% Wahrscheinlichkeit
auch morgen da, mit 30 % W. aber nicht.
Wenn sie heute nicht da sind, dann sind sie mit 90% W. morgen auch nicht da,
nur mit 10% W. kommen sie morgen.

Dieser Zusammenhang wird durch die Übergangsmatrix beschrieben:

• A := matrix([[0.7, 0.3], [0.1, .9]])

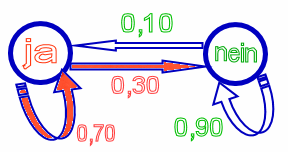
A heißt "stochastische Matrix".
Die Zeilensummen stochastischer Matrizen müssen 1 sein.
Entsprechend gibt es auch "Zustandsvektoren" als stochastische Vektoren.
Sie sind Zeilenvektoren mit Zeilensumme 1.
(0.6 0.4) bedeutet dann, dass heute mit 60% Wahrscheinlichkeit Handwerker
da sind, mit 40% nicht. Es ist die Verteilung der Zustände heute.
Wie sieht dann die Verteilung der Zustände morgen aus?

• v:=(x,y)->matrix([[x,y]]): v(x,y)

Es wird günstigerweise ein Vektor v als Funktion von x und y definiert.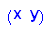

• v(0.6,0.4)

Zur Beantwortung der Frage muss man v mit A multiplizieren: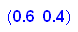

• v(0.6,0.4)*A

Morgen ist dann die Verteilung der Zustände 46% für ja, 54% für nein.

• v(0.6,0.4)*A^2

Dies ist die Verteilung übermorgen.

• v(0.6,0.4)*A^i $ i=3..6

Dieses in den folgenden Tagen. Nun betrachten wir Wochen:

• v(0.6,0.4)*A^(i*7) $ i=1..3

Da scheint sich ja eine stabile Verteilung zu bilden. Wie versuchen: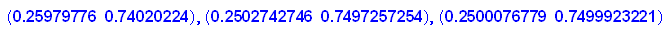

• v(0.25,0.75)*A

Das heißt: auf Dauer werden 25% der Tage Handwerker da sein, 75% der Tage nicht.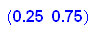
Der Vektor (0.25, 0.75) ist ein Eigenvektor der Matrix A. Wenn man ihn mit A multipliziert,
kommt er selbst wieder heraus.
Allgemein heißt ein Vektor v Eigenvektor zum Eigenwert k, wenn gilt v*A=k*v.
Der obige Vektor ist also Eigenvektor zum Eigenwert k=1.
Eigenwerte und Eigenvektoren kann man "von Hand" oder mit CAS bestimmen.
Eigenwerte "von Hand" siehe ganz unten.
Erst mit CAS, hier mit MuPAD:

• linalg::eigenvalues(A)

1 ist also tatsächlich ein Eigenwert.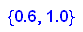
Der zugehörige Eigenvektor erfüllt:

• v(x,y)*A=v(x,y)

• solve([0.7*x+0.1*y=x,0.3*x+0.9*y=y, x+y=1],[x,y])

Das war mit Abschreiben. Automatisch: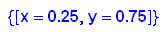

• grenz:=solve([op(v(x,y)*A,1)=x,op(v(x,y)*A,2)=y,x+y=1],[x,y])

Da ist als die stabile Zustandsverteilung herausgekommen.

• gv:=matrix([[op(op(op(grenz),1),2),op(op(op(grenz),2),2)]])

• gv*A

---------------------------------------------------------------------------------------------------------------------------------
Allgemeine Betrachtungen:

• Aalg:=matrix([[p,1-p], [1-q,q]])

• linalg::eigenvalues(Aalg)

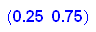
Alle stochastischen 2x2-Matrizen haben den Eigenwert 1.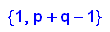

Das Eigenvektorkonzept ist für Spaltenvektoren von rechts konzipiert.
Darum kippen wir die Matrix und das Ergebnis.

• alles:=linalg::eigenvectors(linalg::transpose(Aalg))

• subs(subs(alles, p = 0.7), q = 0.1)

Eigenvektoren sind beliebig skalierbar. Mit Faktor 3/4 ergibt sich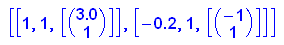
(1/4 , 3/4) als stochastischer Eigenvektor zum Eigenwert 1.
Der andere Eigenvektor ist in diesem Thema nicht deutbar.
---------------------------------------------------------------------------------------------------------------
Allgemein

• solve((1-q)/(1-p)*fak+fak=1,fak)

• fak:=factor((factor((1-q)/(1-p)+1)^-1))

• simplify(subs(subs(fak, p = 0.7), q =0.9))

Stabile Verteilung ist also allgemein: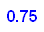

• gva:=v((1-q)/(1-p)*fak,fak)

• gva:=simplify(gva)

Nachrechnen als Probe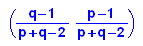

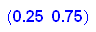
• test:=gva*Aalg-gva

• test:=simplify(%)

• subs(subs(gva*Aalg-gva, p = 7/10), q = 9/10)

• factor(op(test,1));factor(op(test,2))

------------------------------------------------------------------------------------------------------
Potenzen von A

• A^2

• A^i $ i=1..4

• A^i $ i=5..7

• AG:= matrix([[0.25, 0.75], [0.25, .75]])
  

• gv*AG

---------------------------------------------------------------------------------------------------------------------
Allgemein Potenzen von A

• AGalg:=matrix([[op(gva)], [op(gva)]])

• test1:=op(gva*AGalg-gva,1)

• simplify(factor(test1)),simplify(factor(op(gva*AGalg-gva,2)))

Tatsächlich konvergiert die Folge A^n gegen die Matrix,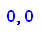
die aus der stabilen Verteilung als zwei Zeilenvektoren gebildet wird.

---------------------------------------------------------------------------------------------------------
Eigenwerte "von Hand":
v*A=k*v soll gelten, k heißt dann Eigenwert.
Also muss v*A-k*v=0 sein. Damit man v ausklammern kann, muss man die
Einheitsmatrix EE zuhilfe nehmen.
v*(A-k*E)=0 . Dies ist eine Vektorgleichung, bei der der Nullvektor herauskommen soll,
man sagt auch: es ist ein homogenes Gleichungssystem.
Nichttriviale Lösungen kommen aber nur dann zustande, wenn die Determinante
der Matrix A-k*EE =0 ist.

• Ma:=matrix([[a,b], [c,d]])

• linalg::det(Ma)

Bei 2x2-Matrizen ist die Determinate die Differenz aus den Diagonal-Produkten.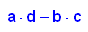

• EE:=matrix([[1,0], [0,1]])

• A-k*EE

• linalg::det(A-k*EE)  //Charakteristisches Polynom

• expand((-k+0.7)*(-k+0.9)-0.1*0.3=0) //zu Fuß

• solve(%=0,k)

Die Nullstellen des Charakteristischen Polynoms sind die Eigenwerte.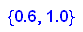

• expand((p-k)*(q-k)-(1-p)*(1-q)=0)

• solve(%,k)

[Stochastik] [MuPAD] Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  Nov. 2004, update 16. November 2004

Internetadressen dieses Web-Verbundes [www.doerte-haftendorn.de]    [haftendorn.uni-lueneburg.de/mathe-lehramt]     [haftendorn.uni-lueneburg.de/ing-math]