www.mathematik-verstehen.de © Prof. Dr. Dörte Haftendorn		Link zum Buch Site-Info
	https://mathe.web.leuphana.de/analysis/ortslinie-leitlinie.htm [Analysis]    [Interaktiv-Info, vor allem für Applets]  [Computer]

Eulersche e-Funktion und Logarithmen

Klingelbrett	Hinführung e-Funktion, interaktive Begründung Theoretische Herleitung dieses Vorgehens Logarithmus-Funktion Logarithmengesetze Basis-Umrechnungen, Ableitung bei Basis a Logarithmen-Umrechnungen Ableitung von ln e als Grenzwert e als Reihe
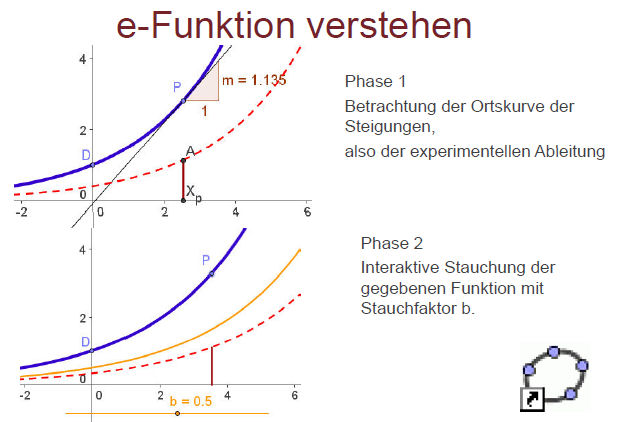
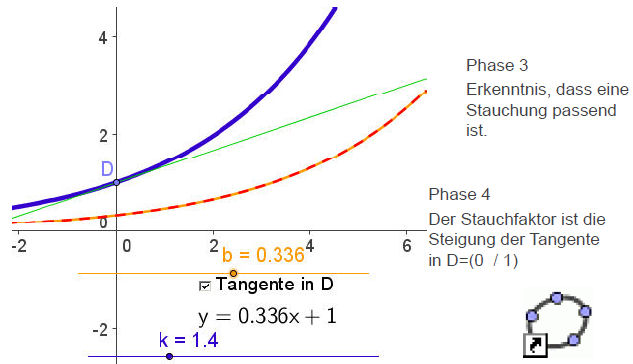
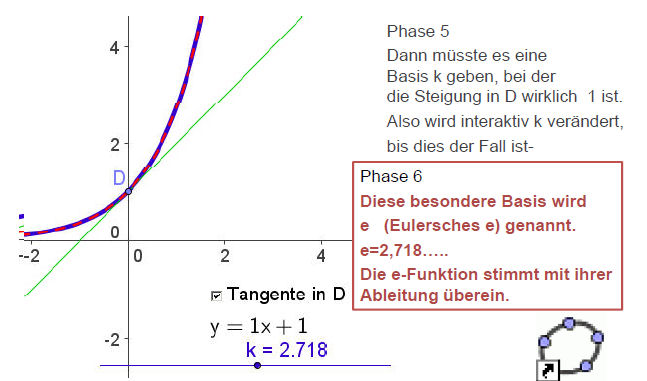
Hinführung	Interaktive Hinführung zur der besonderen Basis Didaktische Anmerkung: Vorher sollte möglichst klar sein, wie man die Ableitungskurve als Ortslinie erzeugt. Dies sind die Folien 10-13 aus dem Vortrag auf der GDM-Tagung Münster 2013 Ortslinie als Leitlinie   Handzettel   download
Theorie	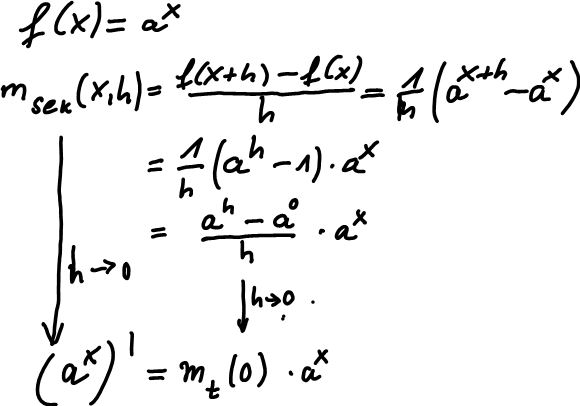Theorie, auf der obiges Vorgehen beruht. Bildet man für eine Exponentialfunktion (a>0) an der Stelle x den Differenzenquotienten, so kann man aus dem Term a^x ausklammern. Der verbleibende Term ist als Differenzenquotient an der Stelle 0 auffassbar. Er hat also die Bedeutung: Sekantensteigung der Exponentialfunktion an der Stelle 0, d.h. im Punkt (0,1). Sein Grenzwert existiert offenbar, denn er ist die Tangentensteigung an der Stelle 0. Damit existiert auch der Grenzwert des Differenzenquotienten an der Stelle x, also die Ableitung an der Stelle x. Sie ist also proportional zum Funktonswert a^x und der Proportionalitätsfaktor ist mt(0). Damit ist gesichert, das man nach der Basis suchen kann, die mt(0)=1 erfüllt. Diese Basis definiert die Eulerschezahl e. Es gilt dann 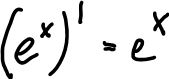. e=2.718281828459045..... Achtung: Man kann ein mathematisches Objekt wie e nur an einer Stelle definieren, alle anderen Eigenschaften müssen dann bewiesen werden. Manchmal wird e über andere Egenschaften definiert, dann ist diese Ableitungseigenschaft nachzuweisen. Die oben vorgeführte Vorgehensweise ist m.E. die einzige, die mit schulischen Mitteln einsichtig ist.
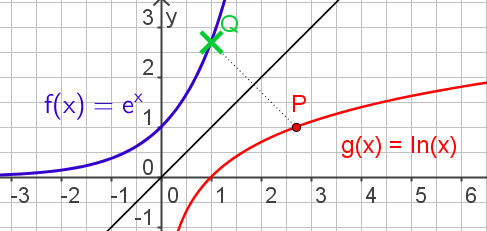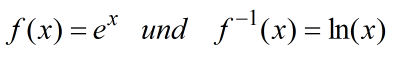
Logarithmus	Die Umkehrfunktionen der Exponentialfunktionen heißen Logarithmusfunktionen. Ihre Graphen gehen durch Spiegelung an der Winkelhalbierenden aus den Graphen der Exponentialfunktionen hervor. Am wichtigsten ist das Paar: e-Funktion vs. ln-Funktion Merke: Allgemein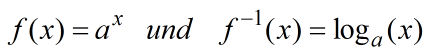
Logarithmengesetze	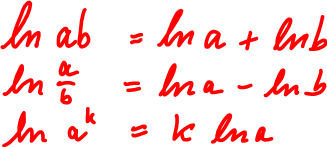Diese Formeln gelten für alle Logarithusfunktionen. Beweise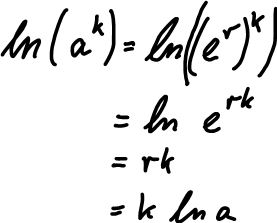
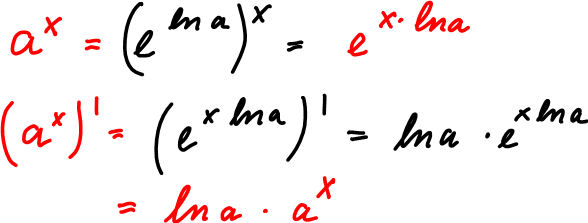
Umrechnungen Basiswechsel Ableitung	Im Vergleich zum Abschnitt "Theorie" zeigt sich, dass die Steigung der Exponentialfunktionen y=a^x im Punkt (0/1) den Wert ln a hat.
Log-Umrechnung ln-Ableitung
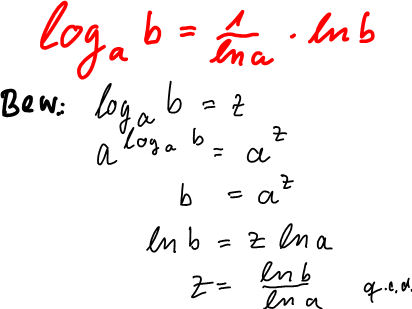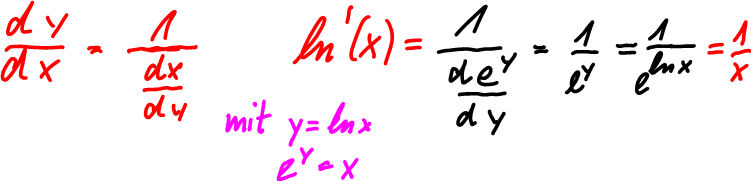
Grenzwert	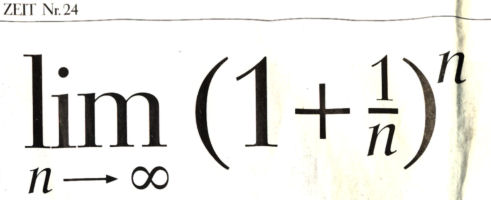Dieser Grenzwert existiert und ist der Wochenzeitung DIE ZEIT eine riesige Überschrift wert. Der Grenzwert ist die Eulersche Zahl e.
Reihe	Dieses ergibt sich aus der Taylorreihe für die e-Funktion

© Prof. Dr. Dörte Haftendorn www.mathematik-verstehen.de	[Analysis][Interaktiv-Info, vor allem für Applets]  [Computer]  Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  März 2013, update 12. März 2013	Site-Info Link zum Buch
	www.leuphana.de/matheomnibus       www.doerte-haftendorn.de https://mathe.web.leuphana.de     http://www.mathematik-sehen-und-verstehen.de