Analysis 3d Leitseite URL haftendorn.uni-lueneburg.de/mathe-lehramt/analysis/3d/3d.htm       © Prof. Dr. Dörte Haftendorn

Download des MuPAD-Notebooks (10 KB)     Save Link Taget As..., Verküpfung speichern unter... Download als pdf (270 KB) Analysis 3D Rotations-Paraboloid- der Hut
Mathematik mit MuPAD 2.5, Prof. Dr. Dörte Haftendorn 12.11.03 Version vom 12.11.03
LLLLLLLLLL-------Level 1-------LLLLLLLLLL

Ein Notebook mit 3D-Graphen ist riesig, 5 MB, bzw 16 MB!!!,wenn die Graphen verfeinert sind.
Da das ganz unakzeptabel ist, sind im Notebook die Ausgaben gelöscht (mit Notebook/Ausgaben löschen).
Nun muss man mit Notebook/Evaluiere/alle Eingaben alles neu auswerten.
Eine nach unten geöffnete Parabel soll sich drehen

• plotfunc2d(4-x^2,x=-2..2)

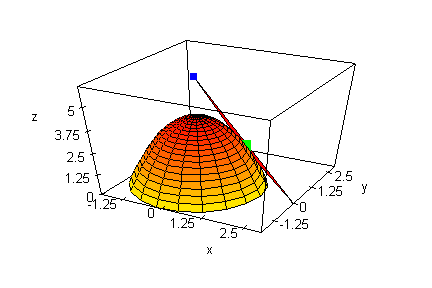
Die Hochachse soll die z-Achse sein. Dann sehen wir hier die x-z-Ebene.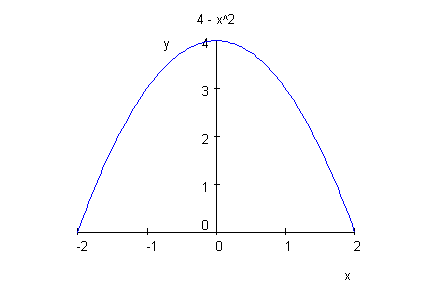
In der y-z-Ebene muss es genauso aussehen. Also:

• f:=(x,y)->(4-x^2-y^2);

• plotfunc3d(f(x,y),x=-2..2,y=-2..2);

Edel-Graphikim 3D-Viewer eine 3D-Graphik doppelt anklicken,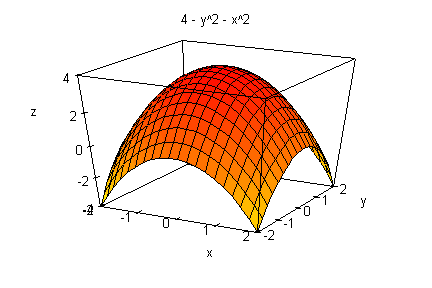
Bearbeiten, ---->im 3D-Viewer öffnen.
Dort mit frei drehen, mit rechter Maustaste evt. Objekteigenschaften ändern.

Schnitte senkrecht zur y-Achse, also y=konstant

• schnitte_y_c:=(f(x,k/2) $ k=0..4)

• plotfunc2d(schnitte_y_c,x=-2..2)

Schnitte senkrecht zur x-Achse, also x=konstant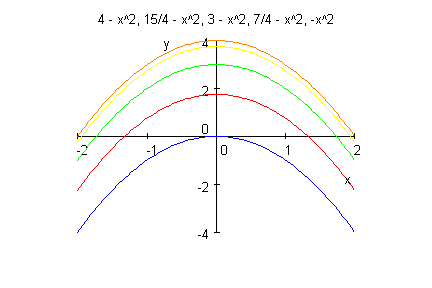

• schnitte_x_c:=(f(k/2,y) $ k=0..4)

• plotfunc2d(schnitte_x_c,y=-2..2)

Wie erwartet sind alles verschobene Parabeln.
Es sind die Gitterlinien der 3D-Graphik.
------------------------------------------------------------------------------------
LLLLLLLLLL-------Level 2-------LLLLLLLLLL
Eigentlich möchte man aber auch die Kreise sehen, die
durch die Rotation entstehen.
Dazu muss man für x und y Polarkoordinaten nehmen: x=r cos (phi) und y=r sin (phi) .
Für z nimmt man den ursprünglichen Funktionsterm, geschrieben mit r, also z = f ( r ).
Nun braucht man das Werkzeug für Raumflächen. Zuerst wird ein Graphik-Objekt
mit dem Namen "rund" erzeugt, das dann von der universellen Funktion plot dargestellt wird.

• rund := plot::Surface3d(
    [r*cos(phi), r*sin(phi),4-r^2], phi = 0..2*PI, r =0..2):
  plot(rund);
  

Nun sind die Kreise als die Höhenlinien zu sehen.
Man sieht hier auch noch besser, dass sich eine Parabel gedreht hat.
Nicht vergessen: Im 3D-Viewer ansehen!!!!!!!!!
------------------------------
Für die Höhenlinien allein, wie auf der Wanderkarte, wählt man z=konstant .

• kreise:=(f(x,y)-k  $ k=0..4)

• hoehenlini:=plot::implicit([kreise],x=-2..2,y=-2..2 ):
  plot(hoehenlini, Scaling=Constrained)

Als Alternative für die Höhenlinien allein gibt es ein Extrawerkzeugin allen CAS.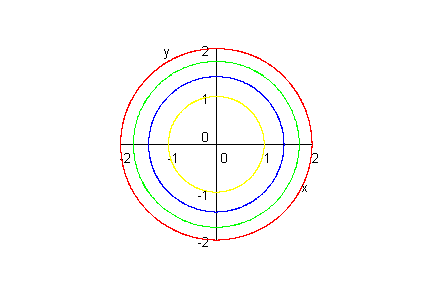
Hier ist es aber nicht so gut. Man weiß auch nicht, in welcher Höhe sie Kreise genommen sind.

• hoehenlinien:=plot::contour([x,y,f(x,y)],x=-2..2,y=-2..2, Grid=[80,80]):
  plot(hoehenlinien, Scaling=Constrained)

------------------------------------------------------------------------------------
LLLLLLLLLL-------Level 3-------LLLLLLLLLL
Nun soll im Punkt P(1,1,z) eine Ebene gezeichnet werden.

• f(1,1)

Die z-Koodinate von P ist 2.
Verändere a so, dass in 3D-Viewer eine Tangentialebene zu sehen ist.

• a:=2.5:
  p1 := plot::Point([a,0,0]):
  p2 := plot::Point([0,a,0]):
  p3 := plot::Point([1, 1,2]):
  eb1 := plot::Polygon(p1,p2,p3,Filled=TRUE): 
  plot(rund,eb1,p1,p2,p3);
  // Unbedingt im 3D-Viewer ansehen !!!!!!!!!!!!!!!

------------------------------------------------------------------------------------
LLLLLLLLLL-------Level 4-------LLLLLLLLLL
Nun soll im Punkt P(1,1,2) eine Tangentialebene bestimmt werden.
Die Steigung nimmt man aus der ursprünglichen Parabel.
Dann ist ein wenig Geometrie in Raum fällig.
Besser sind die Methoden der 3D-Analysis, da hilft der Gradient (siehe Level 5).

• diff(4-x^2,x)

• subs(%,x=sqrt(2))

• ebene:=2*x+2*y+z=d:
  subs(ebene,x=1 ,y=1, z=2)

• d:=op(%,1)

• ebene

Die Achsen-Durchstoßpunkte sind leicht auszurechen: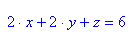

• p1 := plot::Point([3,0,0]):
  p2 := plot::Point([0,3,0]):
  p3 := plot::Point([1, 1,2], Color = RGB::Green, PointWidth = 80):
  p4 := plot::Point([0,0,6], Color = RGB::Blue, PointWidth = 50):

• eb1 := plot::Polygon(p1,p2,p3,Filled=TRUE): 
  spur := plot::Polygon(p1,p2,p4, Closed=TRUE,Filled=TRUE): 
  plot(rund,eb1,p4,p3, spur);
  // Unbedingt im 3D-Viewer ansehen !!!!!!!!!!!!!!!

------------------------------------------------------------------------------------
LLLLLLLLLL-------Level 5 -------LLLLLLLLLL
Nun soll im Punkt P(1,1,2) eine Tangentialebene mit den Methoden der
3D-Analysis bestimmt werden.
Partielle Ableitungen

• fx:=diff(f(x,y),x);fy:=diff(f(x,y),y);

• subs(fx,x=1);subs(fy,y=1);

Die Tangentialebene in P0=[x0,y0,z0] ist
z-z0 = fx (x-x0) + fy (y-y0)
also:

• z-2=-2*(x-1)-2*(y-1)

• %+2

• tang:=plot::Function3d(6-2*y-2*x,x=0..2,y=0..2):
  p3 := plot::Point([1, 1,2],Color = RGB::Green, PointWidth = 90):
  stange:=plot::line([1, 1,2],[3, 3,3]):
  plot(rund,tang,p3,stange):

[Analysis]  [3D] Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  Nov. 2003, update 06. August 2012

Internetadressen dieses Web-Verbundes [www.doerte-haftendorn.de]    [haftendorn.uni-lueneburg.de/mathe-lehramt]     [haftendorn.uni-lueneburg.de/ing-math]