Mathematik Verstehen Dörte Haftendorn: Analysis 3D Sombrero

Analysis 3d Leitseite URL haftendorn.uni-lueneburg.de/mathe-lehramt/analysis/3d/3d.htm © Prof. Dr. Dörte Haftendorn

Download des MuPAD-Notebooks (12 KB) Save Link Taget As..., Verküpfung speichern unter... Download als pdf (95 KB)

Analysis 3D Sombrero
Mathematik mit MuPAD 2.5, Prof. Dr. Dörte Haftendorn 8.07.99 Version vom 13.11.03
-------------------------------------------------------------
Ein Notebook mit 3D-Graphen ist riesig, 5 MB, bzw 16 MK!!!,wenn die Graphen verfeinert sind.
Da das ganz unakzeptabel ist, sind hier die Ausgaben gelöscht (mit Notebook/Ausgaben löschen).
Nun muss man mit Notebook/Evaluiere/alle Eingaben alles neu auswerten.
Sombrero

somb:=(x,y)->cos(x^2+y^2)/(1+x^2+y^2);

plotfunc3d(somb(x,y),x=-3..3,y=-3..3);

Edel-Graphikim 3-D-Viewer eine 3d-Graphik doppelt anklicken,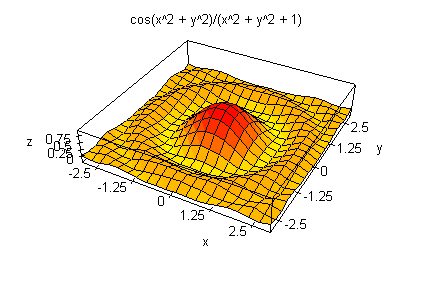
Bearbeiten, ->im 3d-Viewer öffnen

sombrero := plot::Surface3d(
[r*cos(phi), r*sin(phi), cos(r^2)/(1+r^2)], phi = 0..2*PI, r =0..2.8):
plot(sombrero);

Untersuchung der Erzeugenden Funktion
Zähler-Baustein

plotfunc2d(cos(x^2),x=-4..9);

plotfunc2d(cos(x^2),1/(1+x^2),somb(x,0),x=-1..3);

Extremum im Bereich [2,3]
Vorhersage: Das Extremum muss kurz vor dem Maximum der Kosinusfunktion liegen.
Und das liegt bei x^2=2 PI

solve(x^2=2.0*PI)

float(%)

somb(2.5,0)

Genauere Bestimmung: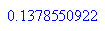

diff(cos(r^2)/(1+r^2),r);
solve(%=0,r);

Dieses lässt sich nur numerisch lösen.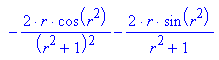

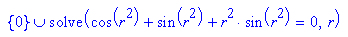
numeric::fsolve(1+w*sin(w)=0,w=5..8);

op(op(%,1),2)

maxstelle:=sqrt(%)

somb(maxstelle,0)

Nochmal Zeichnung alle zusammen:

plotfunc2d(1/(1+x^2),cos(x^2)/(1+x^2),-1/(1+x^2),x=-4..9);

Untersuchung der Taylorreihen
h(x)=1/(1+x^2), g(x)=1/(1+x)

t1:=taylor(cos(x),x=0,6)

t2:=taylor(cos(x^2),x=0,8)

t3:=taylor(1/(1+x),x=0,6)

t4:=taylor(1/(1+x^2),x=0,8)

t2*t4

tay:=expr(%)

plotfunc2d(f(x,0),tay,x=0..3,y=-1..1)

Der Konvergenzradius ist kleiner als 1. Bgründung: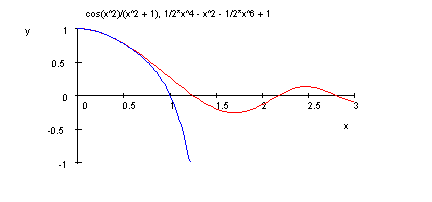
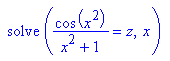
g hat bei x= -1 einen Pol.
Darum hat h im Komlexen bei z=i einen Pol.
Im Komplexen gibt es immer Konvergenzkreise, die bis zur ersten problematischen
Stelle reichen. Dieser Kreis bestimmt dann auch den reellen Konvergenzradius,
der ist dann also nur 1.

Vorschlag für einen exponentiellen Sombrero

some:=(x,y)->(cos(x^2+y^2)*exp(-(x^2+y^2))):some(x,y);

plotfunc3d(some(x,y),x=-2..2,y=-2..2);

sombrex := plot::Surface3d(
[r*cos(phi), r*sin(phi), cos(r^2)*exp(-r^2)], phi = 0..2*PI, r =0..2.8):
plot(sombrex);

Volumenberechnung
Sinnvoll wäre die Integration bis zur 1. Nullstelle

sqrt(PI/2)

nullstelle:=float(%)

und Bestimmung als
Rotationsvolumen um die y-Achse. Dazu bräuchte man aber die Umkehrfunktion.
Das geht aber nicht, das die Gleichung transzendent wird.

solve(f(x,0)=z,x)

Alternativ könnte man Zylinderringe der Dicke dr aufsummieren.
Näherungsweise nehme ich dünne Wände der Dicke dr

numeric::int(2*PI*r^2*f(r,0),r=0..nullstelle)

Probe mit Vergleichskörper: Kegel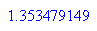

PI*(5/4)^2*1/3

keg:=float(%)

Da der Kegel ganz im Sombero liegt, hätte ein kleinerer Wert herauskommen müssen.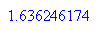

Näherungsparabel

p:=x->1-k*x^2

solve(p(1.25)=0)

plotfunc2d(1-16/25*x^2,f(x,0),x=-1.4..1.4)

Umkehrfkt. der Parabel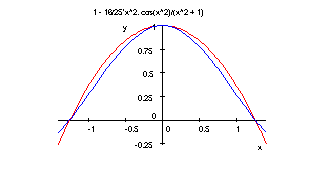

solve(z=1-16/25*x^2, x)

fk:=op(%,2)

PI*int(fk^2,z=0..1 )

par:=float(%) //Volumen unter der Parabel

zyl:=PI*25/16 //Volumen der umfassenden Zylinders

zylf:=float(%) //Es ist erwartungsgemäß doppelt so groß
//wie das Parabelvolumen und dreimal so groß wie das Kegelvolumen.

   





[Analysis]  [3D] Inhalt und  Webbetreuung ©Prof. Dr. Dörte Haftendorn  Nov. 2003, update 14. August 2011


Internetadressen dieses Web-Verbundes [www.doerte-haftendorn.de]    [haftendorn.uni-lueneburg.de/mathe-lehramt]  
  [haftendorn.uni-lueneburg.de/ing-math]