 Download des MuPAD-Notebooks Save Link Taget As..., Verküpfung speichern unter...
Download des MuPAD-Notebooks Save Link Taget As..., Verküpfung speichern unter...
 Iteration an der logistischen Parabel, mit Web-Graphen
Iteration an der logistischen Parabel, mit Web-Graphen
Mathematik mit MuPAD-2, Prof. Dr. Dörte Haftendorn 10.10.2001 Version vom 27.4.03
________________________________________________________________________________
Inhalt....: Iteration an der logistischen Parabel, mit Web-Graphen
Kategorie.: Erklärungsblatt
Mathematik: Rekursive Folgen
MuPAD.....: 2.5.0
Datum.....: 2003-04-27
Autoren...: Dörte Haftendorn <Haftendorn@uni.leuphana.de>
Funktionen: @@ iterative Aufrufe, plot, solve, einige Listenbefehle als Blackbox
________________________________________________________________________________
- delete(r):logistParabel:=x->(r*x*(1-x));
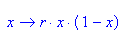
- r:=2.5: plotfunc2d(logistParabel(x),x,x=0..1,Scaling=Constrained)
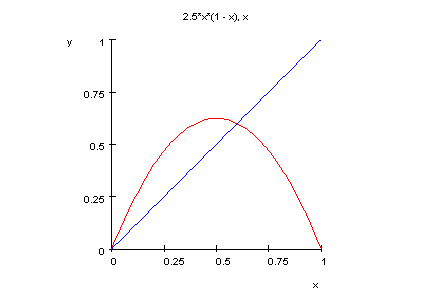

- r:=2.5:start:=0.1:n:=5:start,(logistParabel@@i)(start) $ i=1..n-1;
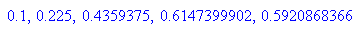
Fixpunkt der Folge scheint xfix=0.6 zu sein. Nachweis durch Fixpunktberechnung
- solve(logistParabel(x)=x,x);
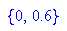
Da r inzwischen den Wert 2.5 hatte, ist nun gleich der Fixpunkt für dieses r herausgekommen.
Will man den Fixpunkt in Abhängigkeit von r,
so muss man r mit delete(r) wieder freigeben.
- delete(r):fix:=solve(logistParabel(x)=x,x);
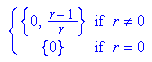
- xfix:=(r-1)/r //von Hand abgeschrieben
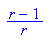
- simplify(logistParabel(xfix)); //Probe
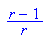
- delete(r):lpAbl:=simplify(logistParabel'(x)); //Ableitung
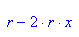
- Steigung_xfix:=subs(lpAbl,x=xfix);//Steigung im Fixpunkt
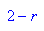
- subs(Steigung_xfix,r=2.5);
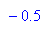
Die Steigung im Fixpunkt ist flach (Betrag keiner 1). Daher ist x=0.6 wirklich anziehender Fixpunkt für r=2.5.
Allgemein kann man hier sehen, dass flache Steigungen für 1<r<3 zustande kommen.
Für r=3 ist xfix=2/3 gerade auch noch anziehender Fixpunkt mit sehr langsamer Konvergenz. Das kann man hier nicht
sehen, sondern durch Beobachten des graphischen Verfahrens (siehe unten).
Für größere Werte von r treten zuerst zwei Häufungswerte auf, dann vier usw.,
Für etwa r=3.6 erfolgt der Eintritt in chaotisches Verhalten.
Web-Graphen
- delete(r):f:=x ->(r*x*(1-x)):f(x)
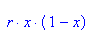
- r:=3.4:start:=0.1:n:=20:Folge:= start,float((f@@i)(start)) $ i=1..n-1:
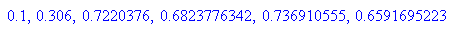
- //-----------------------------------------------------------
whPkte:=zip([Folge],[Folge],plot::Point):
olge:=Folge:delete(olge[1]):olge:
Folg:=Folge: delete(Folg[n]):Folg:
tragPkte:=zip([Folg],[olge],plot::Point):
allePkte:=_concat([plot::Point(start,0)],zip(whPkte,tragPkte,id)):
treppchen:=plot::Polygon(op(allePkte)):
xmin:=0:xmax:=1:ymin:=0:ymax:=1://von Hand eintragen
traeger:=plot::Function2d(f(x),x=xmin..xmax,Color=RGB::Blue):
wh:=plot::Function2d(x,x=xmin..xmax,Color=RGB::Black):
//----------------------------------------------------------
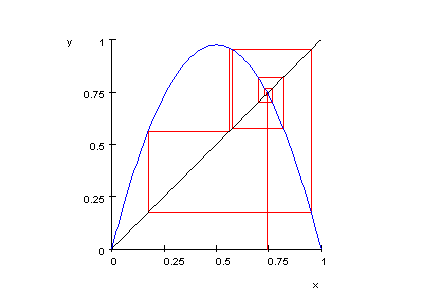
- plot(treppchen,traeger,wh,Scaling=Constrained):
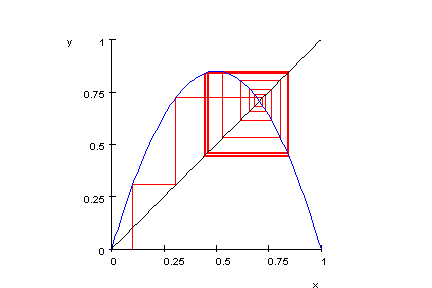
Beispiel aus dem chaotischen Bereich
- delete(r):xfix,Steigung_xfix
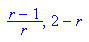
- subs(xfix,r=2.5);subs(Steigung_xfix,r=2.5);

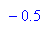
- r:=3.9: subs(xfix,r=3.9); subs(Steigung_xfix,r=2.5);
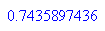
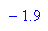
- r:=3.9:start:=0.7436:n:=20:Folge:= start,float((f@@i)(start)) $ i=1..n-1;
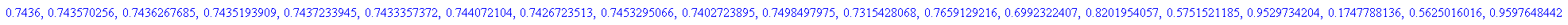
Obwohl der Startwert schon vier sichere Ziffern hatte,
ist nach knapp 20 Iterationen nichts mehr von dem guten Start übrig.
- //----------------------------
whPkte:=zip([Folge],[Folge],plot::Point):
olge:=Folge:delete(olge[1]):olge:
Folg:=Folge: delete(Folg[n]):Folg:
tragPkte:=zip([Folg],[olge],plot::Point):
allePkte:=_concat([plot::Point(start,0)],zip(whPkte,tragPkte,id)):
treppchen:=plot::Polygon(op(allePkte)):
xmin:=0:xmax:=1:ymin:=0:ymax:=1://von Hand eintragen
traeger:=plot::Function2d(f(x),x=xmin..xmax,Color=RGB::Blue):
wh:=plot::Function2d(x,x=xmin..xmax,Color=RGB::Black):
//-------------------------------
- plot(treppchen,traeger,wh,Scaling=Constrained)
//Hierfür nochmal ab whPkte:= bis wh:= auswerten

Internetadressen dieses Web-Verbundes [www.doerte-haftendorn.de] [haftendorn.uni-lueneburg.de/mathe-lehramt]
[haftendorn.uni-lueneburg.de/ing-math]


 [LBS-Mathe] [Analysis] ]
[LBS-Mathe] [Analysis] ]
Inhalt und Webbetreuung Prof. Dr. Dörte Haftendorn  Apr. 2003, update 14. August 2011
Apr. 2003, update 14. August 2011
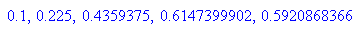
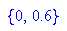
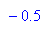

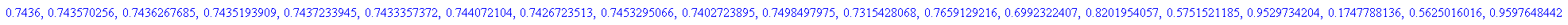
![]()
![]()
![]()
![]() [LBS-Mathe] [Analysis] ]
[LBS-Mathe] [Analysis] ]![]() Apr. 2003, update
Apr. 2003, update