[Analysis] [3d-Analysis]
| www.mathematik-verstehen.de | |||
[Analysis] [3d-Analysis] | |||
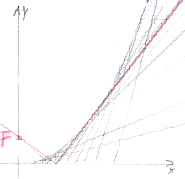
Die Schar der anderen Kante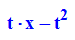
Animation, doppel-klicken, Player starten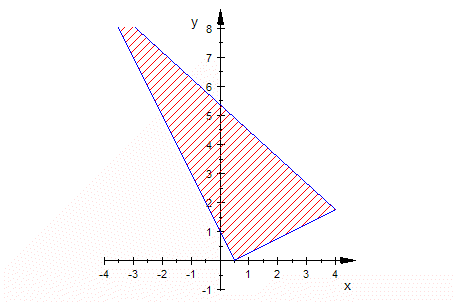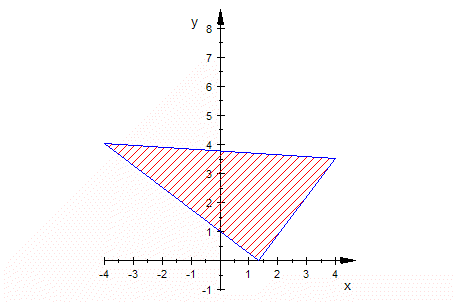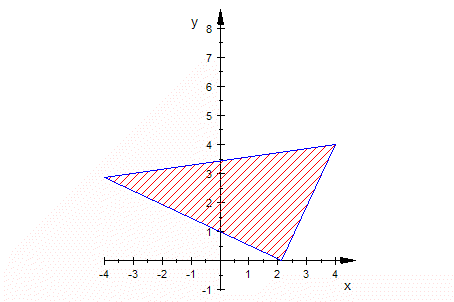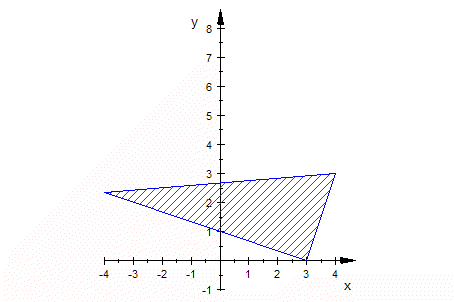

Hüllkurve aus Extremal-Idee.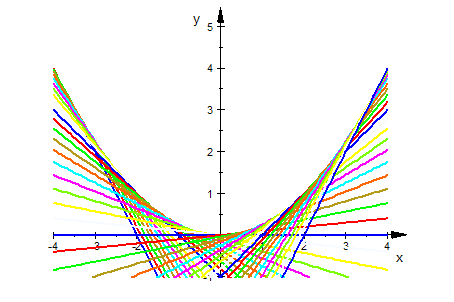

Animation, doppel-klicken, Player starten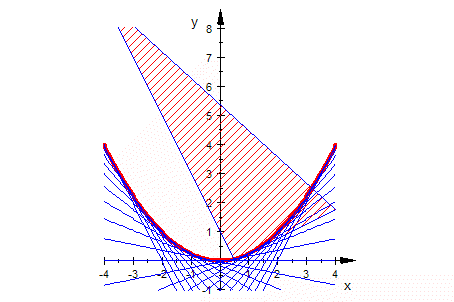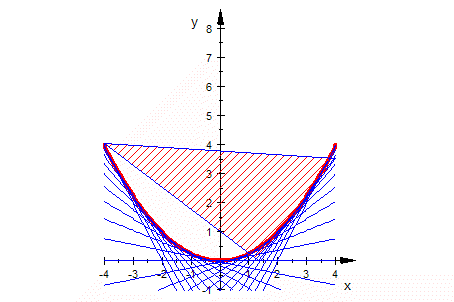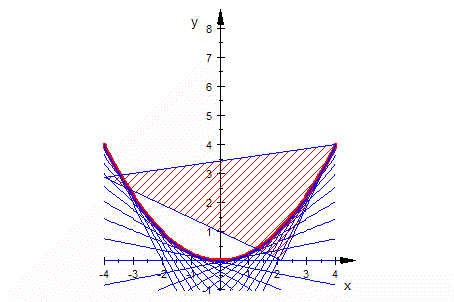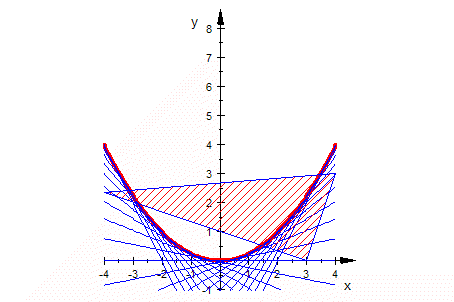

Animation, doppel-klicken, Player starten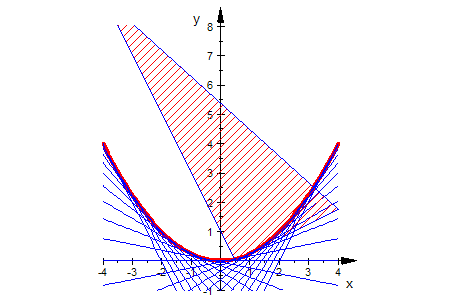

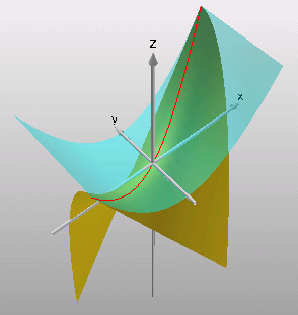
Kurve der Extrema im Raum=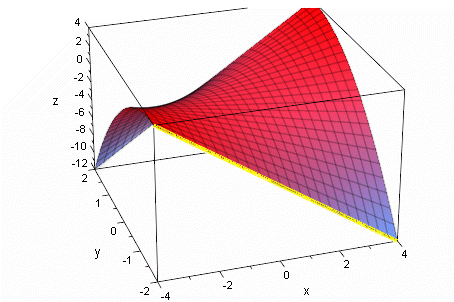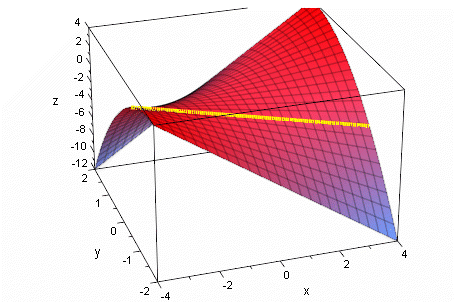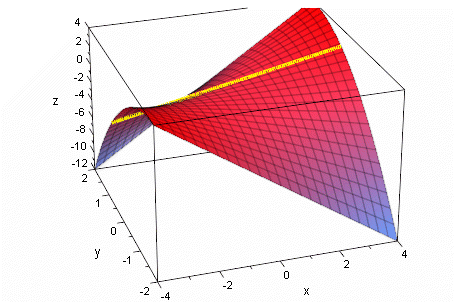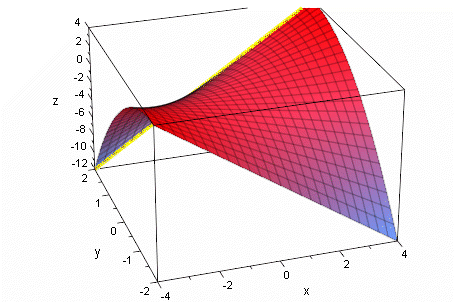

Die folgende Graphik war aus MuPAD 2.5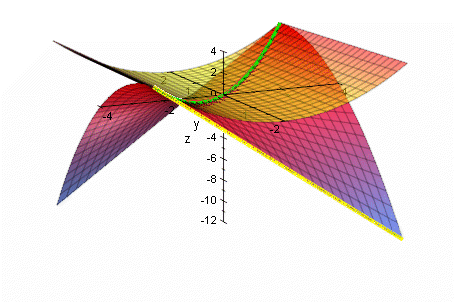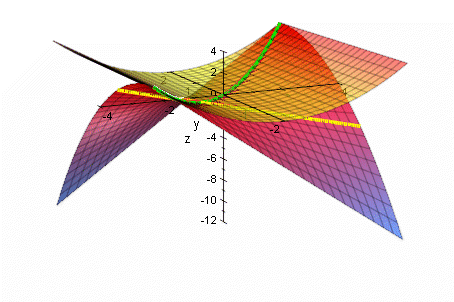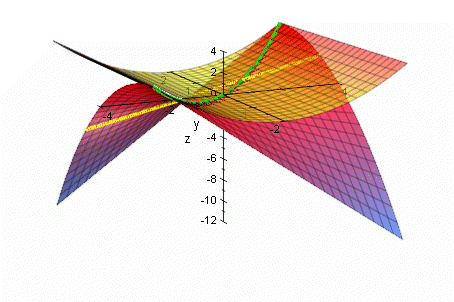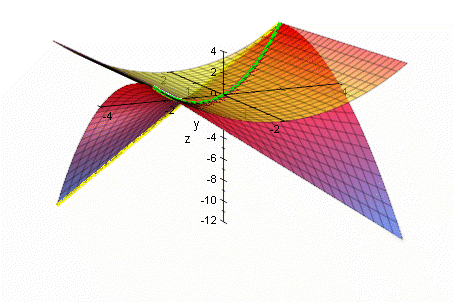

https://mathe.web.leuphana.de http://mathematik.uni-lueneburg.de |