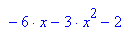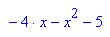Download des MuPAD-Notebooks (650 KB) Save Link Taget As..., Verküpfung speichern unter...
 Matheblatt von Martina aus Österreich, leichter Teil Nr.1 bis Nr. 7
Matheblatt von Martina aus Österreich, leichter Teil Nr.1 bis Nr. 7
1. Die Punkte A (1/-4) B (2/-8) und C (-1/-2) liegen auf der Parabel p1.
Bestimmen Sie deren Gleichung und zeichnen Sie p1.
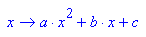
- solve({p(1)=-4,p(2)=-8,p(-1)=-2},{a,b,c})
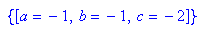
Die gesuchte Parabel ist p1: y= - x^2 - x - 2
- plotfunc2d(-x^2-x-2,-4,-8,-2,x=-1..2)
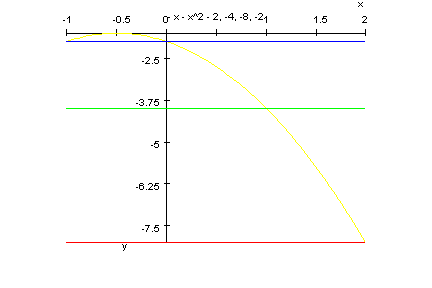
 2. Der Punkt D (3/2) und der Scheitel S2 (4/1) bestimmen die Parabel p2.
Geben Sie die Gleichung von p2 an und zeichnen Sie p2
2. Der Punkt D (3/2) und der Scheitel S2 (4/1) bestimmen die Parabel p2.
Geben Sie die Gleichung von p2 an und zeichnen Sie p2
- p2:=x->t*(x-4)^2+1 // Scheitelform
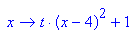
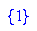
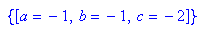
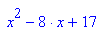
Die gesuchte Parabel ist p2: y= - x^2 - 8x +17.
- plotfunc2d((x-4)^2+1,2,x=-1..7)

 3. Die Normalparabel p3 berührt die x-Achse und geht durch den Punkt E (2/-2,25).
Bestimmen Sie p3 (2 Lösungen) und zeichnen Sie beide Parabeln.
3. Die Normalparabel p3 berührt die x-Achse und geht durch den Punkt E (2/-2,25).
Bestimmen Sie p3 (2 Lösungen) und zeichnen Sie beide Parabeln.
- p3:=x->-(x-a)^2 // Scheitelform
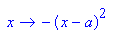
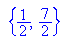
- p3a:=x->-(x-1/2)^2; p3b:=x->-(x-7/2)^2

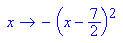
- expand(p3a(x));expand(p3b(x));
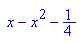
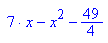
Die gesuchte Parabeln sind p3a: y= - x^2 - x -1/4 und p3b: y=-x^2+7x-49/4.
- plotfunc2d(-(x-1/2)^2,-(x-7/2)^2,-2.25,x=-2..6)
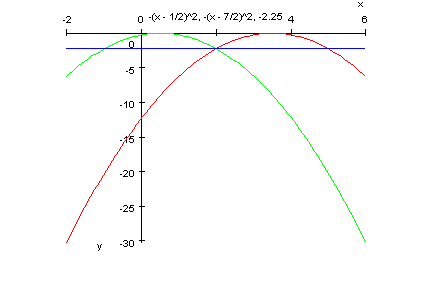

4. Die Parabel p4 schneidet die y-Achse bei y0 = -2 und hat den Scheitel S4 (-1/-1).
Bestimmen Sie die Gleichung von p4 und zeichnen Sie p4.
- p4:=x->t*(x+1)+1 //Scheitelform
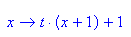
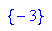
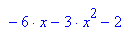
Die gesuchte Parabel ist p4: y= - 3 x^2 - 6x - 2.
- plotfunc2d(-3*(x+1)^2+1,x=-2..2)
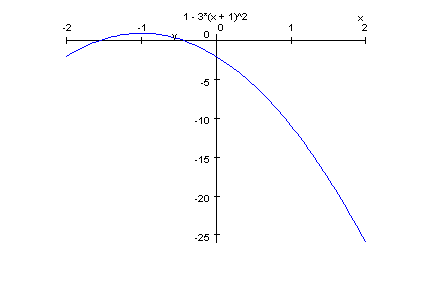

5. Die Parabel p5 mit dem Scheitel S5 (-2/-1) berührt die Gerade g5: y = -2x-4;
Geben Sie Gleichung von p5 an, berechnen Sie Koordinaten des
Berührpunktes T und zeichnen Sie p5 und T.
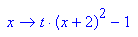

Berührung heißt, dass es nicht zwei Schnittpunkte gibt sondern genau einen.
Also muss die Wurzel Null sein, also muss t= - 1 sein.
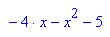
Die gesuchte Parabel ist p5: y= - x^2 -4x -5.
- plotfunc2d(-(x+2)^2-1,-3/2,-2*x-4,x=-4..1)


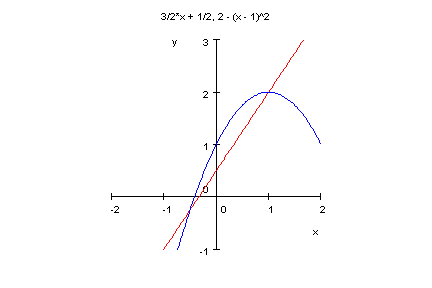
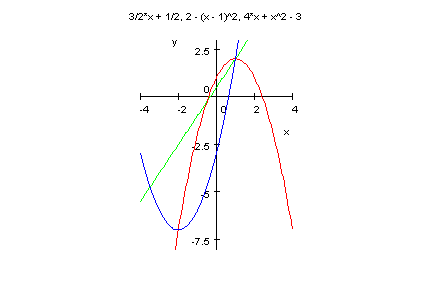
6. Die Parabel p6: y = - (x-1)2 + 2 schneidet die Gerade g6: y = 1,5x + 0,5.
Zeichnen Sie p6 und g6. Bestimmen Sie die Koordinaten der
Schnittpunkte P1 und P2 rechnerisch.
- p6:=x->-(x-1)^2+2; g6:=x->3/2*x+1/2;
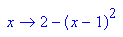
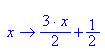
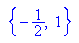
- g6(-1/2);g6(1); /* Ordinaten */


Schnittpunkte S1(-1/2 ; -1/4) und S2(1; 2)
- plotfunc2d(g6(x),p6(x),x=-2..2, y=-1..3,
Scaling=Constrained)

7. Die Parabel P6 schneidet die Parabel p7: y = x2 + 4x 3 in P3 und P4.
Bestimmen Sie P3 und P4 rechnerisch und zeichnen Sie p7 bei 6. ein.
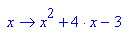
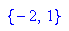
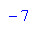

Schnittpunkte: P3(-2/-7); P4(1,2)
- plotfunc2d(g6(x),p6(x),p7(x),x=-4..4, y=-8..3,
Scaling=Constrained)



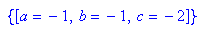

2. Der Punkt D (3/2) und der Scheitel S2 (4/1) bestimmen die Parabel p2. Geben Sie die Gleichung von p2 an und zeichnen Sie p2
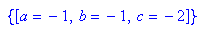
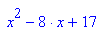

3. Die Normalparabel p3 berührt die x-Achse und geht durch den Punkt E (2/-2,25). Bestimmen Sie p3 (2 Lösungen) und zeichnen Sie beide Parabeln.