www.mathematik-verstehen.de © Prof. Dr. Dörte Haftendorn		Link zum Buch Site-Info
	URL  https://mathe.web.leuphana.de/analysis/parabeln/parabeln.htm [Analysis]  [Parabeln]  [Computer]

Download des MuPAD-Notebooks (700 KB)     Save Link Taget As..., Verküpfung speichern unter... Matheblatt von Martina, vom schwierigeren Teil die Nr.8

8. Die Parabelschar p8: y = x2 (2k + 1) x + 2k + 2,25 wird betrachtet (k ist reelle Zahl). a) Bestimmen Sie den Trägergraphen der Parabelscheitel und zeichnen Sie ihn. b) Zeichnen Sie die Parabel für k = 0; -0; 1 c) Geben Sie die Nullstellen von p8 in Abhängigkeit von k an (Fallunterscheidung).

• p8:=x->x^2-(2*k+1)*x+2*k+9/4

Einsetzen einige k, damit erstmal ein Eindruck entsteht.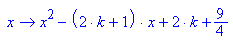

• alle:=(subs(p8(x),k=ks) $ ks=-3..3)
  

• plotfunc2d(alle)

Man sieht: die Parabeln schneiden sich wohl alle in einem Punkt,
die Scheitel liegen für größere Werte von Betrag(k) immer weiter außen.
Sicher ist: Alle Parabeln sind nach oben göffnet, denn vor x^2 steht stets +1.
Es sind daher alle verschobene, unverformte Normalparabeln.
Vermutung: Die Kurve, die die Parabelscheitel trägt, ist eine nach unten geöffnete Parabel
Evt. ist deren Scheitel in dem gemeinsanen Punkt.

Rechnerische Untersuchungen:
Ableitung:

• p8'(x)

• solve(2*x-2*k-1=0,x)    /*Scheitelstelle*/

• p8(k+1/2)    /* Ordinate dazu*/       

• expand(%)

• kurve:=plot::Curve2d([k+1/2,k-k^2+2],k=-3..3);plot(kurve)

In dem Kurven-Zeichen-Befehl steht die "Parameterdarstellung" der Kurve der Scheitel.
Aus x=x(k) und y=y(k) eliminiert man k und erhält die "kartesische Darstellung" y=g(x) der Kurve.

• solve(x=k+1/2,k) 

• kurventerm:=subs(p8(x),k=x-1/2)

• plotfunc2d(alle,kurventerm)

Das passt also schön.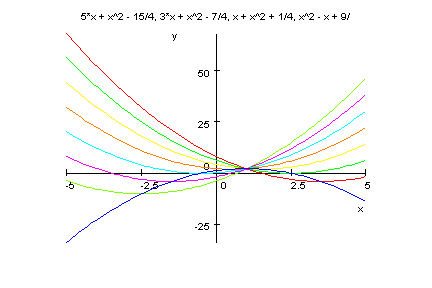
Bestimmung des Schnittpunktes:
Man bestimmt den Schnittpunkt einer Kurve pk mit einer pt.
Wenn ein xs ohne k und t herauskommt, ist gezeigt, dass sich alle Kurven an derselben Stelle schneiden.
Wenn dann auch noch die zugehörige Ordinate kein k enthält, schneiden sie sich in einem Punkt.

• solve(p8(x)=subs(p8(x),k=t),x)

Also für x=1 haben wir eine von k unabhänige Schnittstelle.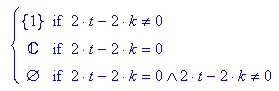
Wenn k=t haben wir dieselbe Kurve zweimal, dann sind alle Punkte gemeinsame Punkte.
Der letzte Fall kann nicht eintreten.

• p8(1)

Also ist S(1; 9/4) gemeinsamer Schnittpunkt aller Kurven.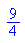

• subs(kurventerm,x=1)

• diff(kurventerm,x)

Also ist die Trägerkurve für die Scheitel tatsächlich eine Parabel mit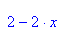
dem ihrem eigenen Scheitel im gemeinsamen Punkt.

Nullstellen:

• solve(p8(x)=0,x)

Es gibt also nur Nullstellen, wenn der Radikand größer Null ist: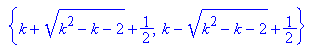

• solve(k^2-k-2=0,k)

• plotfunc2d(k^2-k-2)

Also gibt es nur Nullstellen für x<=-1 und x>=2.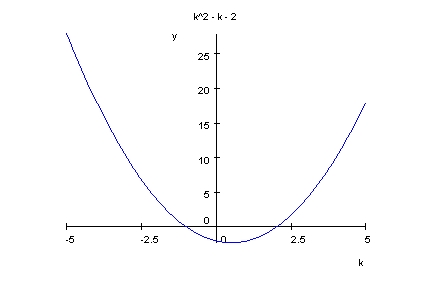
In den "="-Fällen wird die x-Achse berührt.

• wichtige:= (subs(p8(x),k=ks) $ ks=-2..3)

• plotfunc2d(wichtige, kurventerm,x=-4..5,y=-4..5, 
        Scaling=Constrained,GridLines=Automatic)

Man sieht deutlich, dass die Parabeln, die ihren Scheitel im positiven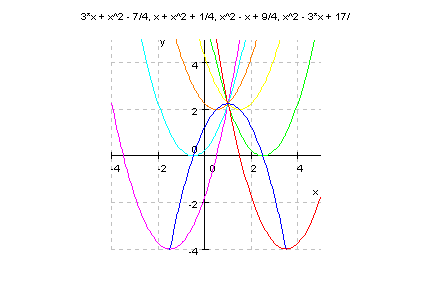
Wertebereich der Trägerkurve der Scheitel haben, keine Nullstellen haben.
Jede Stelle außer x=1 kann aber Nullstelle einer Parabel der Schar sein.
Wenn k betragsmäßig immer größer wird, rückt die eine Nullstelle an 1 heran,
die andere nach außen.

© Prof. Dr. Dörte Haftendorn www.mathematik-verstehen.de	[Analysis]  [Computer] Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  Nov 2002, update 15. August 2011	Site-Info Link zum Buch
	www.leuphana.de/matheomnibus       www.doerte-haftendorn.de https://mathe.web.leuphana.de     http://www.mathematik-sehen-und-verstehen.de