www.mathematik-verstehen.de © Prof. Dr. Dörte Haftendorn		Link zum Buch Site-Info
	URL  https://mathe.web.leuphana.de/analysis/parabeln/parabeln.htm [Analysis]  [Parabeln]  [Computer]

Download des MuPAD-Notebooks (115 KB)     Save Link Taget As..., Verküpfung speichern unter... Matheblatt von Martina, vom schwierigeren Teil die Nr.9

9. Die Parabel P9: y = x2 2 hat die Tangente t1 und t2 die beide durch den Punkt P9 (1/-3,25) laufen.
Berechnen Sie Gleichungen der Tangente und geben Sie Koordinaten der
Berührpunkte T1 und T2 an. Zeichnen Sie p9 und die Tangente t1 und t2.

• p9:=x->x^2-2

Die Gleichung des Geradenbüschels durch P9(1; -13/4) ist:

• t:=x->m*(x-1)-13/4

Die beiden Geraden aus diesem Büschel, die genau einen gemeinsamen Punkt mit der Parabel haben,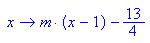
also weder zwei noch gar keinen, sind die gesuchten Tangenten.

• solve(p9(x)=t(x),x)

Also muss der Radikand=0 sein (man sagt auch Diskriminante=0).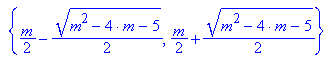

• solve(m^2-4*m-5=0,m)

• t1:=-(x-1)-13/4;t2:=5*(x-1)-13/4

Dies sind die Funktionsterme der beiden Tangenten.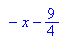

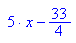
• plotfunc2d(p9(x),t1,t2,x=-5..4,y=-5..6, Scaling=Constrained)

Die Berührpunkte: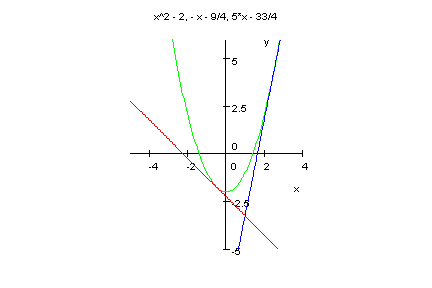

• solve(p9(x)=t1,x);solve(p9(x)=t2,x); 

• p9(-1/2);p9(5/2)

B1(-1/2; -7/4) und B2(5/2; 17/4) sind die Berührpunkte.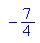

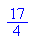
© Prof. Dr. Dörte Haftendorn www.mathematik-verstehen.de	[Analysis]  [Computer] Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  Nov 2002, update 15. August 2011	Site-Info Link zum Buch
	www.leuphana.de/matheomnibus       www.doerte-haftendorn.de https://mathe.web.leuphana.de     http://www.mathematik-sehen-und-verstehen.de