Johanneum Lüneburg	Dr. Dörte Haftendorn Chaos und Fraktale
	Informationssystem
	Mathematik  Chaos

Chaos und Fraktale jetzt neu nur bei Mathematik-Verstehen an der LEUPHANA Uni Lüneburg Dort steht alles, was Sie hier sehen in neuer Gliederung mit deutlich weitergeführten Inhalten

Mandelbrotmengen Apfelmännchen - Grundlage

Das Apfelmännchen wohnt in der komplexen Zahlenebene. und c sind komplexe Zahlen. Grundlage ist die Gleichung

Start bei z_o. Die Folge z_o, z₁, z₂,... nennt man die Bahn (den Orbit) von z_o.
Diese Folge kann man in ihrer Entstehung mit meinem Programm apfjulia © Ha94 beobachten.

B sei der Bereich der komplexen Ebene, in der ein Bild entstehen soll.

Beim Apfelmännchen wird wird jeder Punkt als ein c aufgefaßt.

Wenn dann die Bahn des Ursprungs nach N Schritten beschränkt bleibt, d.h. Abstand 2 vom Ursprung nicht überschreitet, dann wird c schwarz (blau) gefärbt. (Im rechten Bild weiß.) Sonst erhält c eine Farbe, die der Indexnummer entspricht, bei der dieser Abstand 2 überschritten wurde. N heißt Iterationstiefe.

Dabei entsteht das Apfelmännchen mit vielen Farben in der Nähe seines Randes. Im obersten Bild reicht die große Ellipse von -2 bis 1 und von -1,33 i bis +1,33 i .Also verläuft die imaginäre Achse etwa rechts neben der oberen und der unteren großen Knospe entlang. Die reelle Achse ist die Symmetrieachse.

Die anderen Bilder sind Ausschnitte. Dabei ist die Innenfarbe nun hellgrau statt blau.

Die Iterationstiefe war N=5000.

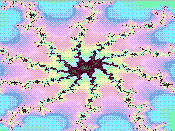Diese beiden Bilder haben den Bereich -0,52330750 + 0.68811162 i links unten -0.52330574 + 0.68811408 i rechts oben
Sie sind also nur 3 Millionstel breit und hoch. Hier zeigt sich, dass die Farben zwar beliebig sind, aber dennoch den Eindruck des Bildes stark beeinflussen. Punkte in einem zusammenhängenden Gebiet einer Farbe habe dieselbe "Fluchtgeschwindigkeit", der Orbit hat also bei derselben Iterationsnummer den Kreis mit Radius 2 verlassen.

Weitere Beispiele

Allgemeinere Mandelbrotmengen (benannt nach B. Mandelbrot) erhält man, wenn man als f(z) andere komlexe Funktionen wählt.
Beispiele sind in meinem Programm apfjulia © Ha94
Diese Bilder sind mit WinFract, der Windowsversion des bekannten Fractint erstellt. Sie können WinFrakt herunterladen.

Chaos und Fraktale jetzt neu nur bei Mathematik-Verstehen an der LEUPHANA Uni Lüneburg Dort steht alles, was Sie hier sehen in neuer Gliederung mit deutlich weitergeführten Inhalten

Autor: © [Dr. Dörte Haftendorn]  Datum März 97. Letzte Änderung am 29. April 2007
[Fächer] [Mathematik] [Chaos] [Webteam] []