Download des MuPAD-Notebooks Save Link Taget As..., Verküpfung speichern unter...
Fraktale mit MuPAD, Wegfraktale rekursiv
Prof. Dr.Dörte Haftendorn, April 03,
________________________________________________________________________________
Inhalt....: Erzeugung von Fraktalen mit rekursiven Prozeduren
Kategorie.: Erklärungsblatt
Mathematik: Fraktale Geometrie
MuPAD.....: 2.5.0
Datum.....: 2003-04-24
Autoren...: Dörte Haftendorn <Haftendorn@uni.leuphana.de>
Funktionen: plot, plot::Turtle, proc
________________________________________________________________________________
LEVEL 1
Als Grundidee werden in Anlehnung an die Lindenmayersysteme einfacheProzeduren definiert:
- F:=proc() begin T::line(x)end_proc:
f:=proc() begin T::move(x)end_proc:
R:=proc() begin T::right(w)end_proc:
L:=proc() begin T::left(w)end_proc:
K:=proc() begin T::push()end_proc:
Z:=proc() begin T::pop()end_proc:
Gr:=proc()begin T::color(RGB::Green)end_proc:
Bk:=proc()begin T::color(RGB::Black)end_proc:
Rd:=proc()begin T::color(RGB::Red)end_proc:
Ma:=proc()begin T::color(RGB::Magenta)end_proc:
Eine rekursive Prozedur, d.h. eine, die sich selbst aufruft, bildet das Fraktal.
Der Initiator (Axiom) erscheint im Rekursionsanfang, in der Abbruchbedingung.
Der Generator wird ausgeschrieben, wobei der Prozedurname(n-1) anstelle von F( ) verwendet wird.
Die Weglänge muss in der Prozedur passend verkleinert werden.
Kochkurve
- koch:=proc(n) local a; begin
a:=x:
if n=1 then F(): return() end_if;
a:=x/3;
koch(n-1):L():koch(n-1):R():R():
koch(n-1):L():koch(n-1):
end_proc:
- x:=1:w:=60:T := plot::Turtle(): /*die Turtle wird erzeugt*/
T::right(90): /* Startrichtung rechts */
koch(3):
plot(T, Axes = None,Scaling=Constrained):
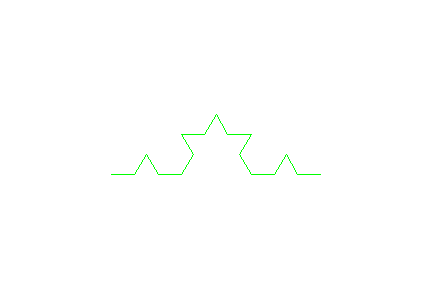
Zweig-Frakal
- zweig:=proc(n) local a; begin
a:=x:
if n=1 then F():return() end_if;
a:=x/3;
zweig(n-1):K():L():Rd():zweig(n-1):Gr():Z():
zweig(n-1):K():R():Bk():zweig(n-1):Gr():Z():
zweig(n-1):
end_proc:
- x:=1:w:=43:T := plot::Turtle():zweig(5):
plot(T, Axes = None):
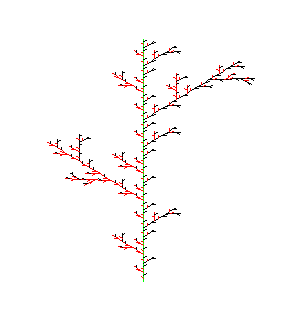
Der Vorteil gegenüber den Lindenmayersystemen ist, dass man auf die erzeugte Turtle zugreifen
und so mehrere Stufen in ein Bild stellen kann.
- x:=27:w:=30:T := plot::Turtle():
K():zweig(1):Z():T::right(90):T::line(6):T::left(90):x:=9:
K():zweig(2):Z():T::right(90):T::line(8):T::left(90):x:=3:
K():zweig(3):Z():T::right(90):T::line(8):T::left(90):x:=1:
K():zweig(4):Z():T::right(90):T::line(10):T::left(90):x:=0.333:
zweig(5):
plot(T, Axes = None/*,Scaling=Constrained*/):
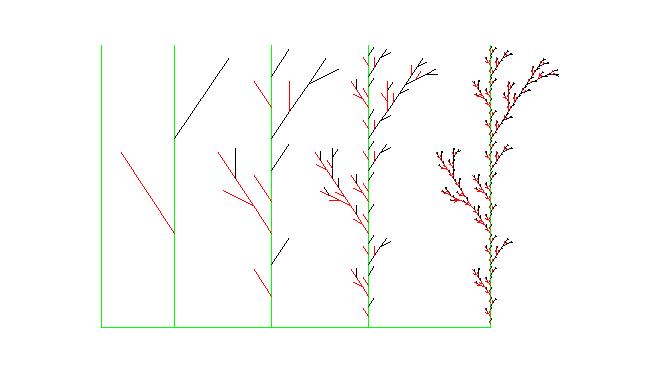
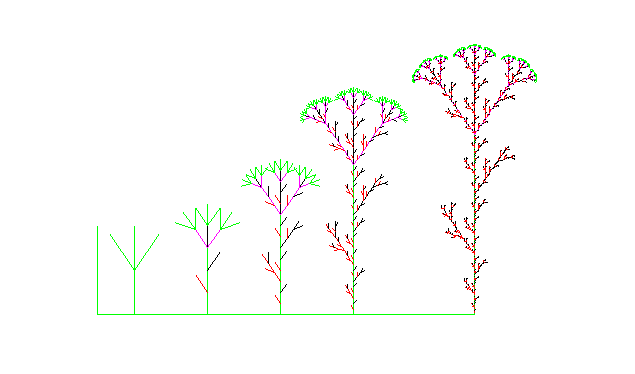
Ein weiterer Vorteil gegenüber den Lindenmayersystemen ist, dass man leichter verschiedene
Fraktale kombinieren und die Farben steuern kann. Auch die Parameter lassen sich von außen steuern.
- delete x:
dolde:=proc(n) local a; begin
a:=x:
if n=1 then Gr(): F();return(): end_if;
a:=x/3;
zweig(n-1):
K():L():Ma():dolde(n-1):Gr():Z():
K(): Bk():dolde(n-1):Gr():Z():
K():R():Ma():dolde(n-1):Gr():Z():
end_proc:
- x:=24:w:=35:T := plot::Turtle():
K():dolde(1):Z():T::right(90):T::line(10):T::left(90):x:=12:
K():dolde(2):Z():T::right(90):T::line(20):T::left(90):x:=6:
K():dolde(3):Z():T::right(90):T::line(20):T::left(90):x:=3:
K():dolde(4):Z():T::right(90):T::line(20):T::left(90):x:=1.5:
K():dolde(5):Z():T::right(90):T::line(33):T::left(90):x:=0.6:
dolde(6):
plot(T, Axes = None/*,Scaling=Constrained*/):
Internetadressen dieses Web-Verbundes [www.doerte-haftendorn.de] [haftendorn.uni-lueneburg.de/mathe-lehramt]
[haftendorn.uni-lueneburg.de/ing-math]
[LBS-Mathe] [Fraktale]
Inhalt und Webbetreuung Prof. Dr. Dörte Haftendorn 
Apr. 2003, update 16. August 2011
Prof. Dr. Dörte Haftendorn 
