Mathe-Lehramt: Kryptographie, El-Gamal-Verfahren

Kryptographie URL
haftendorn.uni-lueneburg.de/mathe-lehramt/krypto/krypto.htm

[Kryptographie] [Algebra] [MuPAD] © Prof. Dr. Dörte Haftendorn

Download des MuPAD-Notebooks Save Link Taget As..., Verküpfung speichern unter...

ElGamal-Verfahren, Public-Key-Verschlüsselung
Kryptographie mit MuPAD,
Prof. Dr.Dörte Haftendorn, Okt.99, Nov 02
-----------------------------------------------------------------------------------
Anton, Berta und Tobi wollen gemeinsam kommunizieren und eine gemeinsame
Schlüsselliste vereinbaren. Tobi bereitet als Grundlage p und g vor.

p:=numlib::prevprime(floor(sqrt(5*10^200)));

p:=11:g:=987:

Sie vereinbaren eine Verschlüsselungsfunktion

delete(f,f_inv,kk,cc): f:=(kk,cc)->(kk*cc):f(kk,cc);

f_inv:=(kk,cc)->(float(cc/kk)):f_inv(kk,cc);

Er teilt dieses allen mit, jeder darf das wissen.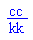
Jeder wählt sich eine beliebige Zahl t als geheimen Schlüssel und
berechnet einen öffentlichenTeil seines Schlüssels:

r:= random((p+1)..5*p): ta:=r();tAnton:=powermod(g,ta,p);

r:= random((p+1)..5*p): tb:=r();tBerta:=powermod(g,tb,p);

r:= random((p+1)..5*p): tt:=r();tTobi:=powermod(g,tt,p);

schluessel:=[tAnton,tBerta,tTobi];//Öffentliche Schlüsselliste

Anton will an Berta und Tobi etwas senden. Er wählt sich eine beliebige Zahl a und berechnet:

r:= random((p+1)..5*p): a:=r();anton:=powermod(g,a,p);

k_AB:=powermod(tBerta,a,p);k_AT:=powermod(tTobi,a,p);

Dieses Antons Kommunikationsschlüssel für Berta und Tobi.
Nun will Anton an die anderen beiden einen Text senden, den nur die beiden lesen können.

numlib::toAscii("Montag im Medley");

m:=77111110116097103032105109032077101100108101121://3-Stellig aufnehmen

A_an_Berta:=f(k_AB,m); A_an_Tobi:=f(k_AT,m);

Berta erhält anton, A_an_Berta,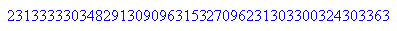
Tobi erhält anton, A_an_Tobi.
Berta berechnet:

k_AB:=powermod(anton,tb,p); vonAnton:=f_inv(k_AB,A_an_Berta);

Tobi berechnet:

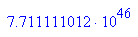
k_AT:=powermod(anton,tt,p);vonAnton:=f_inv(k_AT,A_an_Tobi);

Der Ascii-Text muss noch in Klartext verwandelt werden.
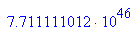
Beim Umwandeln in eine Liste muss man von rechts Dreierpakete machen.

klar:=numlib::fromAscii([77,111,110,116,097,103,032,105,109,032,077,101,100,108,101,121]);

Signatur mit dem ElGamal-Verfahren= DSS= Digital Signature Standard
Anton will seine Nachricht signieren, bekannt sind g, p und sein öffentlicher Schlüssel tAnton:
Er wählt ra teilerfremd zu p-1

repeat
r:= random(2..p-1): ra:=r():
  until gcd(p-1,ra)=1 end_repeat:ra;

kra:=powermod(g,ra,p);

igcdex(p-1,ra);

ra_inv:=op(igcdex(p-1,ra),3); // letztes Element euklid. Algorithmus

if (ra_inv<0) then ra_inv:=ra_inv+p-1: end_if:ra_inv; //Korrektur bei negativem ra_inv

//m:=77;

sa:=modp((m-ta*kra)*ra_inv,p-1);

Anton sendet zu m die digitale Unterschrift (sa,kra);
Tobi will prüfen, ob die Nachricht wirklich von Anton kommt.
Er berechnet

test1:=powermod(g,m,p); test2:=modp(powermod(tAnton,kra,p)*powermod(kra,sa,p),p);

if (test1=test2) then print("Das hat Anton geschrieben: m=".m)
else print("Vorsicht, das ist nicht von Anton Original!") end_if;


"Das hat Anton geschrieben: m=77111110116097103032105109032077101100108101121"

Die von Anton gesendete Signatur ist mit der Nachrricht "verwoben". Sie läßt sich für keine andere
Nachricht verwenden. Wenn die Nachricht verändert wurde, gelingt der Test ebenfalls nicht.

[Kryptographie] [Algebra] [MuPAD]

2001, hier neu 2005, update 14. August 2011

Direkte Internetadressen [www.doerte-haftendorn.de]
[haftendorn.uni-lueneburg.de/mathe-lehramt] [haftendorn.uni-lueneburg.de/ing-math]