Kryptographie URL haftendorn.uni-lueneburg.de/mathe-lehramt/krypto/krypto.htm

[Kryptographie]  [Algebra]  [MuPAD]   © Prof. Dr. Dörte Haftendorn

Download des MuPAD-Notebooks     Save Link Taget As..., Verküpfung speichern unter... Kryptographie, Hash-Funktion
Mathematik mit MuPAD 2, Prof. Dr. Dörte Haftendorn 1.12.02 Version vom 1.12.02
#################################################################################
Eine Hash-Funktion ist ein Einweg-Funktion, die die Nachricht komprimiert. Sie wird im Zusammenhang mit der digitalen Signatur gebraucht.
Foderungen an eine Hashfunktion:
Sie soll möglichst kollisionsresistent sein.
Schwache Kollisionsresistenz liegt vor, wenn das Verändern einer Nachricht so gut wie immer zu einem veränderten Hashwert führt.
Starke Kollisionsresistenz liegt vor, wenn das Konstruieren einer Nachricht mit gleichem Hashwert mindestens so schwierig ist, wie den diskreten Logarithmus modolo p zu bestimmen. #################################################################################

Unten erst das Von - Hand- Beispiel durchführen !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

• delete a,x,p:
  h:=(x,y)->modp(powermod(a,x,p)*powermod(b,y,p),p):

Zunächst muss ein Paar von Primzahlen p und q bestimmt werden,
die p=2 q+1 erfüllen.

• suhash:=proc(start)
            local saat,p,q;
            begin
              repeat
                saat:=random(start div 2..start);
                q:=numlib::prevprime(saat());
                p:=2*q+1;
              until isprime(p) end_repeat;
              return(p,q);
             end_proc :

• pequ:=suhash(123451629872389712) //10^18

• p:=op(pequ,1); q:=op(pequ,2);

Eine Primitivwurzel a von p ist zu bestimmen.
d. h. <a>=zstern(p). Bei der oben erzeugten Konstellation hat zstern die Ordnung p-1=2q.
Damit kommt als Ordnung der Elemente von zstern(p) nur 2 oder q oder p-1 infrage
Wenn also modulo p weder a^2=1 noch a^q=1 gilt, dann erzeugt a zstern(p), ist also Primitivwurzel.
Der Sinn ist, dass die hash-Funktion, die ja a^x enthält, alle Werte aus zstern(p) annehmen kann.

• pw:=proc(p,q)
        local aproc,a;
        begin 
          repeat
            aproc:=random(2..p-1);a:=aproc();
          until  (modp(a*a,p) >1) and (powermod(a,q,p)>1) end_repeat;
          return(a)
        end_proc:

• a:=pw(p,q)

• bproc:=random(p): //beliebige Zahl aus zstern(p)
  b:=bproc();

• h(123456789525251231,897686868686867898)

• h(123456789525251232,897686868686867898)

Schon die Änderung nur einer Ziffer ergibt einen völlig anderen Hashwert.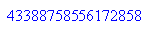

Von Hand- Hashfunktion

• q:=5:   p:=2*q+1; //p prim?, sonst Neuwahl von q

• a:=7: powermod(a,2,p); powermod(a,q,p);

Wenn hier eine 1 steht, Neuwahl von a < p. Nun erzeugt a wirklich zstern(p), Probe dazu: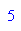

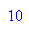
• zstern(p)

• powermod(a,k,p) $ k=1..p-1

Wahl von b aus zstern(p) beliebig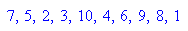

• b:=2: //beliebig<p

Nachricht, aufgeteilt in zwei Blöcke

• x:=8: y:=7:

• ax:=powermod(a,x,p);by:=powermod(b,y,p); modp(ax*by,p);

Die letzte Zahl ist der Hashwert der Nachricht.

Überlegungen zur Kollisionsfreiheit
Will man den 1. Teil der Nachrricht manipulieren, also auch 3 als hashwert erhalten,
so sieht man an der folgenden Zeile, dass es keinen anderen Wert für x gibt, der auch 8 erzeugt.
Das liegt daran dass a Primitivwurzel ist.

• modp(powermod(a,k,p)*by,p) $ k=1..p-1;

• modp(powermod(2,k,p),p) $ k=1..p-1;  //ord(b) ablesbar

Ändert man den ersten und den zweiten Teil der Nachrricht, so kann man 8 erzeugen, in jeder Zeile
kommt 8 genau einmal vor. Z.B. x=4, y=7. Eine solche Kombination ist aber bei großem p nicht zu finden.

• array(1..p-1,1..p-1,[[modp(powermod(a,k,p)*powermod(b,j,p),p) $ k=1..p-1] $ j=1..p-1]);

[Kryptographie]  [Algebra]  [MuPAD]

Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn 2001, hier neu 2005, update 17. September 2005

Direkte Internetadressen [www.doerte-haftendorn.de] [haftendorn.uni-lueneburg.de/mathe-lehramt]    [haftendorn.uni-lueneburg.de/ing-math]