Namensgeheimnis   haftendorn.uni-lueneburg.de/mathe-lehramt/kurven/kegel/kegel.htm       © Prof. Dr. Dörte Haftendorn

Namensgeheimnis der Kegelschnitte
Prof. Dr. Dörte Haftendorn, Version 07/03

•Grundlage: allgemeine Scheitelgleichung der Kegelschnitte

In[111]:=

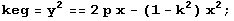
keg = y^2 == 2 p x - (1 - k^2) x^2 ;
•p=Halbparameter=Ordinate im Brennpunkt;  
k=.µ= numerische Exzentrizität
g=Entfernung der Leitgeraden vom Scheitel
Beziehung  g k (k+1)=p
Die Scheitelgleichung folgt aus der Leitgeradenkonstruktion:
"P hat von F die k-fache Entfernung wie von der Leitgeraden g "
(hier der Geraden  x= -g)

In[115]:=

Clear[p, k, g, f] ; f[x_] := (2 p x - (1 - k^2) x^2)^(1/2) g = p/(k (k + 1)) ;

Hyperbel

In[141]:=

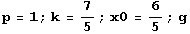
p = 1 ; k = 7/5 ; x0 = 6/5 ; g

Out[141]=

25/84

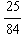
In[142]:=

hyp = ImplicitPlot[y^2 == 2 p x - (1 - k^2) x^2, {x, -1, 3.5}, PlotRange -> {{-g - 0.1, 3.5 ... , 0}] <br />         } <br />] ;     

[Graphics:namensgebung_6.gif]

Parabel

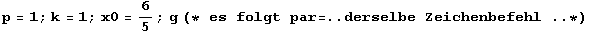
p = 1 ; k = 1 ; x0 = 6/5 ; g (* es folgt par =. . derselbe Zeichenbefehl .. *)

Ellipse

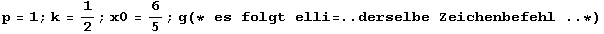
p = 1 ; k = 1/2 ; x0 = 6/5 ; g (* es folgt elli =. . derselbe Zeichenbefehl .. *)

In[144]:=

Show[GraphicsArray[{hyp, par, elli}]] ;

[Graphics:namensgebung_18.gif]

Converted by Mathematica  (July 28, 2003)

[Kegelschnitte] Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  Juli 2003, update 14. August 2011
Internetadressen dieses Web-Verbundes [www.doerte-haftendorn.de]    [haftendorn.uni-lueneburg.de/mathe-lehramt]     [haftendorn.uni-lueneburg.de/ing-math]
Mit Menu im neuen Browserfensterin neuem Fenster