www.mathematik-verstehen.de	http://haftendorn.uni-lueneburg.de	© Prof. Dr. Dörte Haftendorn
http://haftendorn.uni-lueneburg.de/mathe-lehramt/kurven/kegel/kegel.htm [Kurven] [Lehre] [Kegelschnitte] [Höhere Kurven] [Projekt Klasse 8 Johanneum]

Kegelschnitte

Die Kegelschnitte sind die interessanteste Kurvenklasse unter allen algebraischen Kurven mit vielen Bezügen untereinander. Ellipse, Parabel und Hyperbel haben viele gemeinsame Erzeugungsweisen und Eigenschaften, nach denen man die Site gliedern könnte. Aber es gibt auch die speziellen Eigenschaften, die nahelegen, eigene Bereiche für Ellipse, Hyperbel bzw. Parabel zu präsentieren. Hierfür habe mi mich entschieden, aber durch das Kegelsymbol

wird angezeigt, wenn das Angesprochene auch auf die anderen Kegelschnitte übertragbar ist. Man findet das dann sowohl bei der entsprechenden Kurve verlinkt als auch im Bereich "Kegelschnitte algemein".

Einzelkurven		Kegelschnitte allgemein		Übergreifendes
Ellipse Parabel Hyperbel		Kegelschnitte allgemein Fadenkonstruktion Leitgeradenkonstruktion Leitkreiskonstruktion Kegelschnitte aus 5 Punkten Reflexion Namensgeheimnis Aus dem Kegelschneiden Dandelinsche Kugeln Kegelschnitte aus der Gleichung bei Mathe-Vital (Prof. Richter-Gebert TUM München Kegelschnitte als Nullstellen einer Raumfläche bei Mathe-Vital (Prof. Richter-Gebert TUM München		Projekt Klasse 8 Johanneum lohnt besonders bzgl. Konstruktionsbeschreibungen, Geschichte und Anwendungen,.... 1-Seiten-Konzept Zusammenstellung der Beweisseiten Beweise sind oft auch bei den interaktiven Dateien Lesen Sie die Interaktiv-Info Harmonie der Rotationsköper Kegelschnitte und Inversion Meine eigene Abiturarbeit 1966 Ausblick

Hyperbel Fadenkonstruktion

Lichtkegelbilder

Ellipse	Ausführungen, Beweise, Interaktives	Didaktische Bemerkungen
	Ellipse, Konstruktion, Geschichte, Gleichungen
	Lernseite Ellipse als affine Bild des Kreises Ellipse, Scheitelkreiskonstrukion Handzettel im Webplayer download Ellipse aus der gerechneten Stauchung eines Kreises erste Realisierung Ellipse aus der gerechneten Stauchung eines Kreises alternative Konstr. Ellipse als affines Bild des Kreises, konstruiert erste Realisierung Ellipse als affines Bild des Kreises, konstruiert altrernative Realisierung Mit der Tangentenkonstruktion Hierzu meine eigene Abituraufgabe von 1966 Konstr. ohne Tagente in Z.u.L.
Fadenkonstruktion	Ellipse Fadenkonstrukion rein geometrisch Beweis der Fadenkonstruktion nicht im Kurven-Füllhorn < in Kegelschnitt-Allerlei Ellipse Fadenkonstruktion Interaktiv
	Ellipse Fadenkonstruktion (mit Konstr.-Kreisen, aber ohne Ortskuve)
Leitkreiskonstruktion	eigene Leitseite zur Allgemeine Leitkreiskonstruktion
Namensgebung	Eigene Leitseite zur Namensgebung
Stangenkonstruktion	Stangenkonstruktion der Ellipse Asteroide aus der Stangenkonstruktion Rutschende Leiter Rutschende Leiter Stangenkonstruktion in Kegelschnitt-Allerlei Ellipse Stangenkonstruktion, rutschende Leiter, beste Version ist in GeoGebra
Ellipsenzirkel	Ellipsenzirkel Ellipsenzirkel Ellipsenzirkelmit besonderem Phänomen und Vergleich der DGS Ellispenzirkel in Ordnung
Krümmungkreise	Ellipse Krümmungskreise Am schönsten ist die Realisierung in GeoGebra vor allem die interaktive Version Scheitel-Krümmumngskreise der Ellipse nicht im Kurven-Füllhorn Krümmung interaktiv und Herleitung in Bereich Analysis


Parabel	Ausführungen, Beweise, Interaktives	Didaktische Bemerkungen
	Parabel, Konstruktion, Geschichte, Gleichungen,...
	Es gibt nun eine eigene Leitseite zu Parabeln Reflexion an Parabeln ist auf der Leitseite Reflexion untergebracht.
	Der Name der Parabel
	Parabeln tauchen ja überall am leichtesten auf. Z.B. bei Orte erkunden und Wandernder Höhenschnittpunkt Sonst sind sie hier vor allem im Zusammenhang von gemeinsamen Kegelschnitt-Betrachtungen zu finden.
	Parabeln ganz allgemein und auch im Rahmen von Sek I und Analysis

Hyperbel	Ausführungen, Beweise, Interaktives	Didaktische Bemerkungen
	Hyperbel, Konstruktion, Geschichte, Gleichungen,...

	Hyperbeln sind hier vor allem im Zusammenhang von gemeinsamen Kegelschnitt-Betrachtungen zu finden.
Hyperbelzeichner	Hyperbelzeichner, Spektrumbild Umsetzung mit Maßen in GeoGebra Für dieses widersprüchliche Bild sind zwei Interpretationen möglich: 1. Man nimm 2 alpha wirklich als Winkel mit er x-Achse Ausführliche Darstellung der Hyperbelzeichners Hyperbelzeichner 2. Man hält sich an die Größenverhältnisse der Zeichnung und nimmt 2 alpha zusätzlich, also 3 alpha bis zur x-Achse. Ausführliche Darstellung Möchtegern-Hyperbelzeichner


Kegelschnitte allgemein	Ausführungen, Beweise, Interaktives	Didaktische Bemerkungen
	Kegelschnitte im Überblick, Konstruktion, Geschichte, Gleichungen,... Kegelschnitt-Allerlei
Faden- konstruktionen	Ellipse: Abstandssumme von zwei festen Punkten ist konstant. Hyperbel: Abstandsdifferenz von zwei festen Punkten ist konstant. Parabel: Abstand von einem festen Punkt ist derselbe wie von einer festen Geraden. Diese Leitgerade kann man sich als einen ins Unendliche gerückten Fixpunkt vorstellen. Bei der Hyperbel ist der Fixpunkt quasi von der anderen Seite wieder hereingewandert.
Leitgeraden	Leitgeraden Konstruktion aller Kegelschnitte interaktiv Leitgeraden Konstruktion aller Kegelschnitte (Kritik) Beweis zur Leitgeradenkonstruktion Als Rasteraufgabe Leitgeraden Konstruktion aller Kegelschnitte interaktiv mit Erklärungen interaktiv
Leitkreis	"Leitkreis-Konstruktion aller Kegelschnitte" Der Abstand eines Punktes von einem festen Kreis ist derselbe wie der Abstand von einem festen Punkt. Bei Ellipse, Parabel und Hyperbel ist die gegenseitige Lage von Kreis und Punkt verschieden.
	Variante zur Leitkreiskonstruktion: Geometrischer Ort aller Punkte, die von zwei Kreisen denselben Abstand haben. Bei Ellipse, Parabel und Hyperbel ist die gegenseitige Lage der Kreise verschieden.
5 Punkte	Kegelschnitt aus 5 Punkten pur,interaktiv Kegelschnitt aus 5 Punkten DGS, Z.u.L. interaktiv
	Kegelschnitt aus 5 Punkten mit CAS Kegelschnitt aus 5 Punkten mit CAS alte Version
Reflexion	Dies ist nun eine eigene große Leitseite Reflexion geworden.
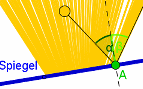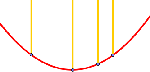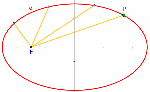
	Schöne Beweis-Seiten gemeinsame Scheitelgleichung, mit Beweis aus der Leitgeradenkonstruktion "Beweis MP-Gl. aus Scheitelgleichung", "Beweis MP-Gl. aus Ellipse-Faden-K.", "Beweis Epsilon, num. Exzentrizität" "alle Parameter der Kegelschnitte"
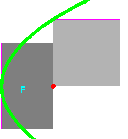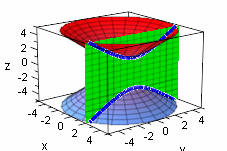
Name	Namensgeheimnis Zusammenhang mit der Leitkreiskonstruktion Namensgeheimnis der Kegelschnitte Grieschische Konstruktion Namensgeheimnis der Kegelschnitte, Griechische Bedeutung Graphen für Klausuren mit dieser Frage
	Ellipse als Schnitt von Ebene und Kegel Pararbel als Schnitt von Ebene und Kegel Hyperbel als Schnitt von Ebene und Kegel Kegelschnitt als geschnittener Kegel Mit Beweisen. Schräger Kegel geschnitten mit x-y-Ebene Ausführlich in Staatsexamensaufgebe Hiermit kann man vektoriell die Kegelschnitte in Mittelpunktslage erzeugen. sichtbar für Ellipse allgemeinter Kegelschnitt Kegelschnitt als geschnittener Kegel
	Kegelschnitte mit DGS !!!Ältere Seite
Dandelin	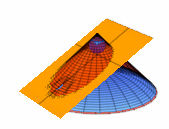Schöne Beweise mit Dandelinschen Kugeln Ellipsensalami, Zylinder schneiden Kegelschnitt-Ellipse mit Dandelinschen Kugeln
Abi 66	Meine eigene Abiturarbeit 1966 Besondere Konstruktion aller Kegelschnitte Interaktiv 1 Interaktiv 2 Hyperbel Interaktiv 3 Ellispe Interaktiv 3 Interaktiv 3 Parabel ungeprüft? Ellipse Beweis (unfertig)
Harmonie	Harmonie der Kegelschnitte , eher ein Thema der Anaysis, es geht um schöne Verhältnisse bei den Rotationskörpern von Ellipse und Hyperbel Inzwischen gibt es auch eine Weiterführung mit höhen Potenzen, auch als Staatsexamensarbeit.
Ausblick	Sehr empfehlenswert ist die Arbeit meines ehemaligen Referendars: Dr. Steffen Hahn: Kegelschnitte mit DGS Staatsexamensarbeit Ballade der Kegelschnitte