Algebraische Kurven URL haftendorn.uni-lueneburg.de/mathe-lehramt/kurven/kurven.htm
[Kurven] [Lehre] [Kegelschnitte] [Höhere Kurven] [Projekt Klasse 8 Johanneum]    © Prof. Dr. Dörte Haftendorn

Ellipsenzirkel
und warum er manchmal nicht funktioniert


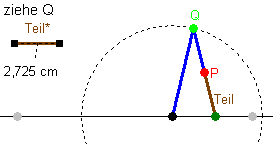
Der Ellipsenzirkel besteht aus zwei gleich langen Stangen s, die in Q beweglich verbunden sind. Ein Schenkel ist bei P unterteilt, Teil=t
Wenn sich Q auf einem Kreis bewegt, beschreibt P eine Bahn. Diese Bahl soll angeblich eine Ellipse sein.
Aufgabe:
Konstruiere den Ellipsenzirkel in deinem DGS.
Versuche es besser zu machen als es hier gelungen ist.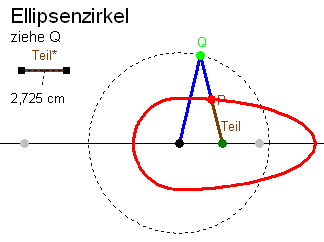
Leider aber ergibt sich mit Euklid-Dynageo dieses hier oben und das ist sicher keine Ellipse.
Was nun????????
Ein Ellipsenzirkel, der keine Ellipsen zeichnet?
Im Folgenden sind mehrere DGS-Werkzeuge getestet und verschiedene Konstruktionsideen verfolgt.
Fazit: Nicht jede Konstruktion oder Beweismethode, die mathematisch richtig ist, ist auch "handwerklich" richtig. Die DGS reagieren verschieden und mit CAS gibt es geschicktes und ungeschicktes Vorgehen.

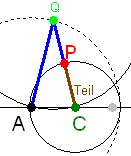Konstruktionsidee I
Der Kreis[Q,QA] erzeugt C und der Kreis[C,t] erzeugt P.
Hierzu sind rechts Realisierungen zu sehen.

Mathematica Lösung mit dieser Idee
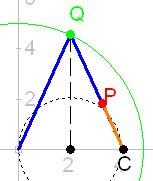Konstruktion II
Erzeugung von C durch Spiegeln an der Senkrechten durch Q

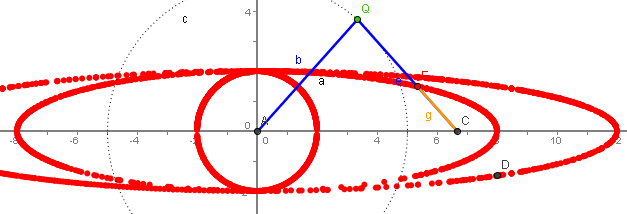Bild aus GeoGebra nach Typ I
Mathematica-Lösung mit Konstruktionsidee I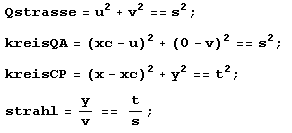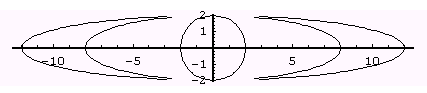

Auch hier ergeben sich mit dieser Idee zuviele Lösungen, Es ist eine Kurve 6.Grades, der Term zeigt das. Das musste man erwarten, weil in dem GeoGebra-Bild Geraden mit 6 Schmittpunkten eingezeichnet werden können.
Mathematica-Lösung mit Konstruktionsidee II


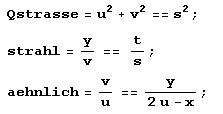Es zeigt sich, dass auch für die algebraische Behandlung dieser Weg viel besser ist.

Begründungen der Probleme mit dem Ellipsenzirkel

falsche OrtskurveDiese erhält man, wenn man nach Idee I konstruiert.
Man erkennt sofort, da ist etwas faul.!!!!!!
Dieses Phänomen kommt dadurch zustande, dass Euklid-Dynageo, wie viele DGS, die beiden Schnittpunkte, die ein Kreis mit einer Geraden hat, nicht unterscheiden kann. A und C tauschen ihre Rollen, wenn Q über den "Nordpol" oder den "Südpol" hinweggezogen wird. Bei GeoGebra wird auch noch der zweite Schnittpunkt des Kreises um C mit der Geraden QC berücksichtigt. Dieses passiert natürlich auch in der algebraischen Behandlung. So ist die von Mathematica gefundene Relation 6. Grades und hat die From der von GeoGebra gefundenen Kurven.
vollständigHier sieht man, dass die zweite Seite nur durch den anderen Schnittpunkt erzeugt wird.

In Zul kann man äußert komfortabel wählen, dass der Schnittpunkt H von M verschieden sein soll. (Re-Maus auf H) Man kann sogar zwischen der richtigen und der falschen Ortslinie hin und her schalten.
Cinderella EllipsenzirkelCinderella unterscheidet grundsätzlich die Schnittpunkte und ist daher in der Lage, hier ohne weitere Vorkehrungen richtig darzustellen.
Cinderella Ellipsenzirkel interaktiv



Mehr zu den Unterschieden der DGS bezüglich der Unterscheidung der Schnittpunkte
[Kurven] [Lehre] [Kegelschnitte] [Höhere Kurven] [Projekt Klasse 8 Johanneum]
Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  (1998), Apr. 2002, update 16. August 2011
Direkte Internetadressen
[www.doerte-haftendorn.de]    [haftendorn.uni-lueneburg.de/mathe-lehramt]