haftendorn.uni-lueneburg.de/mathe-lehramt/computer/dgs/dgs.htm
haftendorn.uni-lueneburg.de/mathe-lehramt/computer/dgs/dgs.htm |
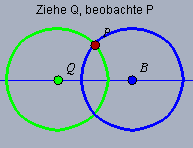 Cinderella ist mathematisch besonders gut konzipiert Cinderella ist mathematisch besonders gut konzipiert Als Prüfsituation schlägt er die im Folgenden realisierte Bewegung mit zwei Kreisen vor: | ||||
| Euklid |
Z.u.L. Z.u.L. Version 2 |
Cinderella |
GeoGebra |
|
| TI-Cabri |
Version 2 |
|||
| Fazit: Sieger dieses "Wettbewerbs" sind Ciderella und GeoGebra Bei Ihnen fürt die stetige Bewegung von Q auch zu einer stetigen Bewegung von P. ZuL leistet das, wenn man Als Eigenschaft von P fordert, dass P verschieden ist von Q und umgekehrt. | ||||
| Gründe: Cinderella verwendet "homgene Koordinaten", bei denen 2D-Punkte als 3D-Vektoren in besonderer Weise dargestellt werden. Die Rechnungen mit den geometrischen Objekten werden in den komplexen Zahlen ausgeführt. Dadurch entgleist in Cinderella nichts, wenn beim Ziehen Schnittpunkte wegfallen oder "durchs Unendliche" gezogen werden. Dieses edle Verhalten hat aber seinen Preis in der schlechteren Zugänglichkeit für Maßoperationen. GeoGebra löst das Problem durch ein geschicktes "Nähe-Konzept", wie mir Markus Hohenwarter ausführlich erkärt hat. | ||||
[www.doerte-haftendorn.de] [haftendorn.uni-lueneburg.de/mathe-lehramt] |