	www.mathematik-verstehen.de	© Prof. Dr. Dörte Haftendorn
https://mathe.web.leuphana.de/geo/geo-plus/inversion/inversion.htm [Computer] [Kurven] [Geometrie] [Höhere Geometrie] [Polarkoordinaten]

Inversion am Kreis oder Kreisspiegelung

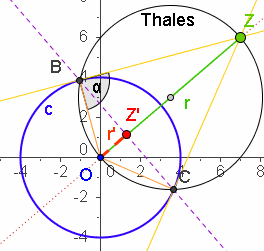
Wir konstruiert man die Inversion?	Definition Arbeitsblatt ab Klasse 8	Konstruktion mit Thales Konstruktion ohne Thales
Tipps für die Einführung	In Euklid-Dynageo gibt es "Kreisspiegelung" als Button. Man das auch als "zu erkundende Blackbox" benutzen. Auch wenn man "Tangenten" als heißen Tipp verrät, ist das zugfest Konstruieren der Tangenten (jedenfalls bei meinen Studierenden) immernoch ein Abenteuer. Aber man lernt viel dabei. In GeoGebra gibt es die Inversion nicht als Befehl, aber die Polare, dann hat man auch schnell den Bildpunkt. 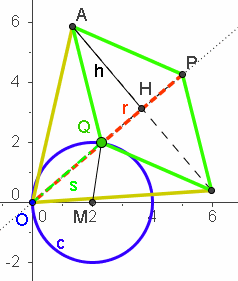Blackbox-Erkundung mit GeoGebra Blackbox-Erkundung mit Euklid-Dynageo
Welche Formel gilt?	r und r' sind also invers zueinander im Sinne der Algebra. Der Beweis ist eine Anwendung das Kathetensatzes auf das Dreieck OZB mit der Kathete OB=k. Ausführliche Seite dazu und zu komplexen Zahlen Inversion und Polarkoordinaten
Bilder von Figuren bei der Inversion	Invertiert man ein Polygon (z.B. mit Euklid-Dynageo) durch Invertierung seiner Eckpunkte, so liegt nahe, die Bildpunkte wieder zu einem Polygon zu verbinden. (Achtung, arge Falle!)	Euklid-Dynageo dazu download
Bilder von Kurven bei der Inversion	Man sollte dann, ggf. nachträglich, das Urbild Z an eine Gerade und andere Kurven binden und die Bilder erkunden lassen. Nun kann die Erkenntnis reifen, dass das Bild eine Polygons gar kein Polygon ist, sondern eine von Kreisbögen begrenzte Figur.	Gerade download Gerade mit Ort download Die Inversen bilder von Geraden sind Kreise durch den Ursprung unten auf der Seite Polygon richtig download
Inversion für Funktionen	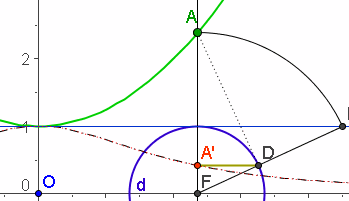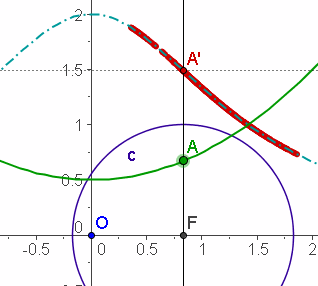Kehrwert-Funktion als Inversion, Extra-Konstruktion rein geometrisch download unter Ausnutzung der Polare download
Inversion und Polarkoordinaten	Inversion und Polarkoordinaten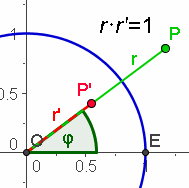 Wählt man als Inversionskreis den Einheitskreis um den Ursprung, dann geht der Punkt P(r,t) in den Punkt P'(1/r, t) über, Die Polarradien sin also Kehrwerte voneinander, der Winkel wird beibehalten. Eine invertierte Kurve ist identisch mit der algebraisch invertierten Kurve. So erklärt sich auch der Name Inversion.
Inversion und Komplexe Zahlen	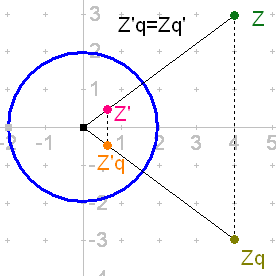Ausführliche schöne Seite dazu Das geometrisch Inverse lät sich bestimmen als das konjugiert-Komplexe des algebraisch Inversen. 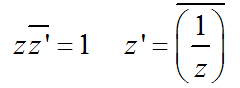Siehe auch den Extrabereich Komplexe Zahlen
Hier folgt eine Zusammenstellung einiger Kurven mit ihrer kartesischen Gleichung und ihrer Polargleichung. Grundsätzlich erhält man sie aus einer x-y-Darstellung durch Einsetzen von x=r cos(phi) und y=r sin(phi) und Auflösung nach r.
Kurven und ihre Inversen	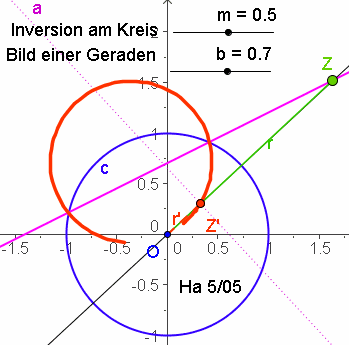Die Polargleichung des Inversen einer Kurve ist das algebraisch Inverse ihrer Polargleichung. Man sieht hier: Geraden und Kreise durch den Urspung sind zueinander invers.
Kegelschnitte Pascalsche Schnecken	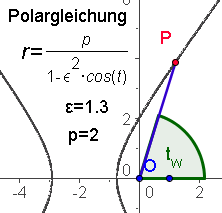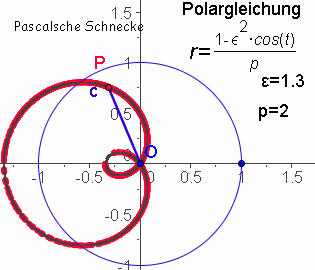Diese Hyperbel hat den Brenn- punkt im Ursprung. Ihre Inversion am Einheitskreis ergibt die Pascalsche Schnecke.
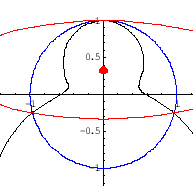
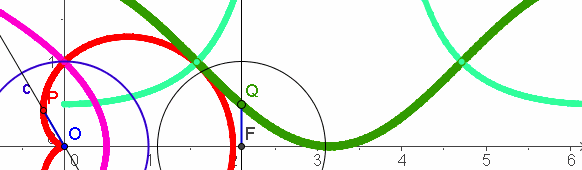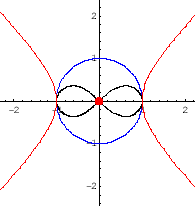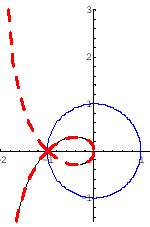Polar- Darstellung und Inversion besser verstehen	Polar-Darstellung und Inversion besser verstehen dazu

Strophoide	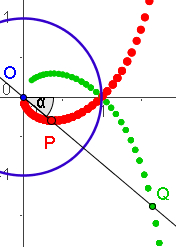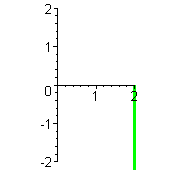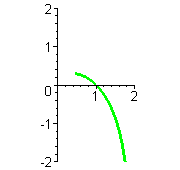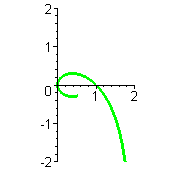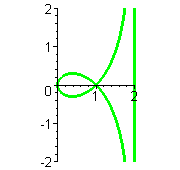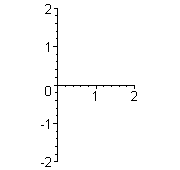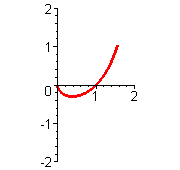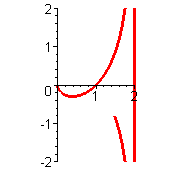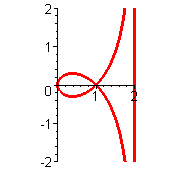Strophoide als analagmatische Kurve, d.h. sie kann bei Inversion in sich selbst übergehen. Extraseite zur Inversion der Strophoide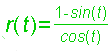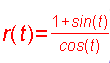
Allerlei	Strophoide, LemniskateStrophoide als analagmatische Kurve, d.h. sie kann bei Inversion in sich selbt übergehen. Lemniskate als Bild einer Hyperbel Ellipsenbilder	Ellipse Invers ohne Ortskurve download Ellipse Invers mit Ortskurve download
Peaucellier-Gelenk Inversor Inversenzirkel		Diese Gelenkkonstruktion setzt eine Kreisbewegung in ein perfekte Geradenbewegung um. Dieses wurde lange für unmöglich gehalten. Peaucellier erfand diesen "Inversor" 1864. Der Inversor von Peaucellier Ohne Orstskurve download Mit Orstskurve download Interessante Panne, die mit de
Inversion von weiteren Kurven