www.mathematik-verstehen.de
Link zum Buch
www.mathematik-verstehen.de |
| Link zum Buch |
|
https://mathe.web.leuphana.de/analysis/polar/polar.htm | ||
| Einführung Erkundung große Erkundungs Aufgaben |
Polar-kartesische Koppelung Vorträge |
Didaktik Werkzeuge |
Analysis Aufgaben Spiralen |
Kurven Rosetten |
| Einführung | 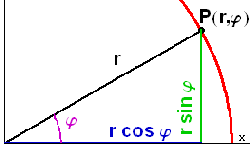 Durch die Graphenzeichner sind heute Polardarstellungen ungeheuer leicht verfügbar. Durch die Graphenzeichner sind heute Polardarstellungen ungeheuer leicht verfügbar. Daher gibt es viele Gründe Ein Pionier in dieser Richtung ist Prof. Günter Steinberg, Oldenburg, der schon vor Jahren ein gutes Buch mit dem Titel "Polarkoordinaten" in die Welt der Mathematik-Lehre gestellt hat. |
| Erkunden |
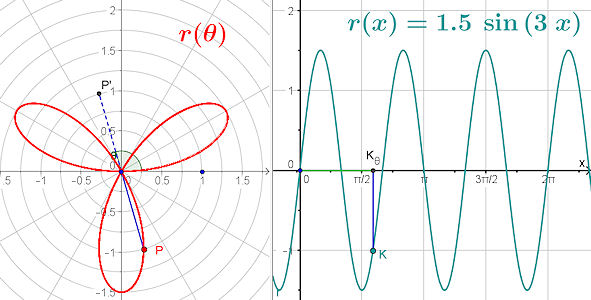 
 Diese Datei kann man für die ganze Arbeit mit Polarkoordiaten nutzen.
Diese Datei kann man für die ganze Arbeit mit Polarkoordiaten nutzen.
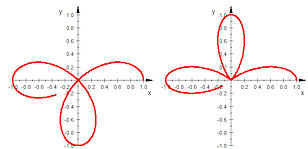 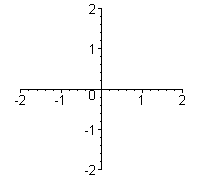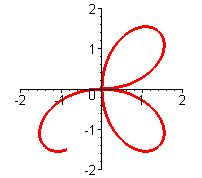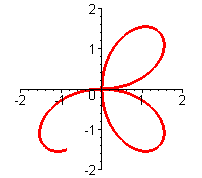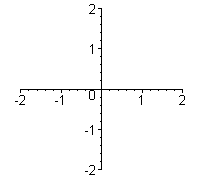
Der Kreis wird zweimal durchlaufen, wenn phi von 0 bis 2PI läft. Dieses Verhalten ist durch die polar-kartesische Sicht gut zu verstehen. |
| große Erkundungs- Aufgaben |  Propeller-Aufgabe Propeller-Aufgabe
Aufgabe: (kurz) Wo kommt der kleine Zipfel her? 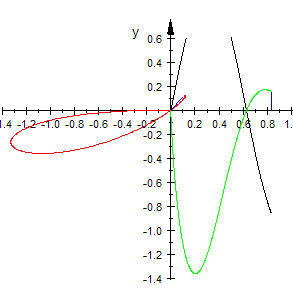 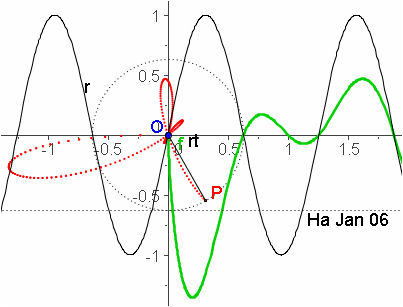 |
| Klausur- Aufgabe |  Schöne Aufgabe für eine Analysis-Klausur Schöne Aufgabe für eine Analysis-KlausurGanze Klausur Dort auch Aufgabe zur Didaktik der Polarkoordinaten |
| Vorträge |
Vortrag auf der GDM-Tagung in Osnabrück am 10.03.06 Aufsatz zum Vortrag in Osnabrück (4 Seiten) Lecture to the Internatinal ProMath-Conference in Lünebeurg 31.08.07 (Problem Solving in Mathmatics Education) |
| Algebraische Kurven Definitionen Rechnungen |
Auf dieser Seite wird auch auf Algebraische Kurven, insbesondereKonchoiden im Allgemeinen eingegangen. Die Gleichung eines Kreises durch den Ursprung, dessen Mittelpunkt auf der x-Achse liegt, kommt vor. Daraus ergeben sich die Polargleichungen der Pascalschen Schnecken. |
| Hundekurve |
Die Version"polar-pur" können Sie durch wegklicken des Fensters Grafik 2 erreichen. |
| Pascalsche Schnecken | Eigene Leitseite für polar-kartesische Darstellung Pascalscher Schnecken Pascalsche Schnecken allgemein Pascalsche Schnecken mit Inversion in Polarkoordinaten |
| Cassinische Kurven | Cassinische Kurven aus Ortskurven und mehr dazu... |
| Rosetten | Eigene Leitseite Rosetten Auch als Einführung oder bals danach geeignet |
| Strophoide Dreiblatt |
Eigene Leitseite Stophoide Eigene Leitseite Dreiblatt ganz ähnlich aufgebaut |
| Didaktik | Die Einbeziehung von Polarkoordinaten ist außerordentlich ergiebig, wenn graphikfährige Taschenrechner (oder andere Computerwerkzeuge) vorliegen.
Insbesondere ist die Betrachtung von kartesischen r-über Phi-Graphen zur Erkärung der Phänomene bei den Polar-Graphen sehr fruchtbar, übt den "Standardstoff" und lässt hier Klausuren auf jedem Niveau von Klasse 10 bis zum Staatesexamen zu. Auch bei Vorhandensein eines Werkzeugs bleibt genug mathematische Substanz, die andererseits aber auch lehrbar und erreichbar ist.
Ausfühliches in den Vorträgen  Schöne Aufgabe für eine Analysis-Klausur, gestellt im Staatsexamen Schöne Aufgabe für eine Analysis-Klausur, gestellt im StaatsexamenGanze Klausur Dort auch Aufgabe zur Didaktik der Polarkoordinaten |
|
| Werkzeuge |  Graphenzeichner als Black-Box: Graphenzeichner als Black-Box:Im Einstellungsmenu des Gerätes , b.z.w. der Software findet sich "Polarkoordinaten" und man stellt die schlichte Frage: "Wie bekommen wir heraus, was das heißen soll?". In Anlehnung an die Erfahrung, dass Geraden, Parabeln, Wurzelfunktionen die schulisch vertrautesten und einfachsten Funktionen sind, lässt man r(θ)=θ u.ä. durch Zeichnen im Graphikfenster untersuchen. Meist bekommen die Lernenden selbst heraus, was "Polarkoordinaten" bedeuten. |
|
|
||
| CAS: Maxima MuPAD |
MuPAD gibt es ja leider nicht mehr. Dennoch kann man aus meinen Erläuterungen für andere CAS, z.B. Maple, lernen. Nun sind da auch Durchläufe und Animation sehr!!!! einfach möglich. Zur Not: alte Version MuPAD 2.5 (web) download auf Anfrage, die Graphik ist ab MuPAD 3 um Klassen besser |
|
| CAS: Mathematica Maple |
und bei der Inversion der Strophoide |
|
| CAS: Derive |  In Derive ist unter dem Menüpunkt In Derive ist unter dem Menüpunkt"Einstellen Koordinatensystem" "polar" auszuwählen. Dann wird das Passende gezeichnet. Hier kann im Spurmodus der Graph mit dem Karo-Zeiger verfolgt werden. In einem weiteren Graphik-Fenster kann man r über phi auftragen und betrachten (Dazu siehe bei Stophoide)  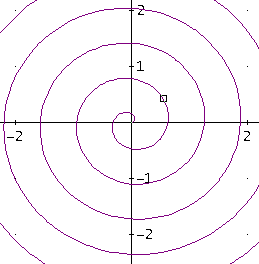 |
|
| Animationen |   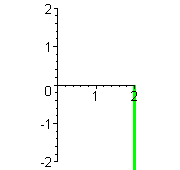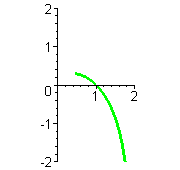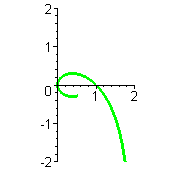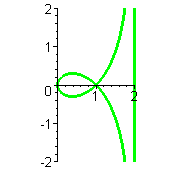 MuPAD und Maple ermöglichen ganz einfach diese Graphen (siehe *.mws) zu erzeugen und als animiertes *.gif-Bild zu exportieren. Für MuPAD steht es in obiger Datei Der zugehörige Befehl für Maple und Interessantes zum Duchlauf der Kurven steht bei der Strophoide | |
| Analysis- aspekte und Aufgaben | Das wichtigste Potential liegt m.E. beim Erkunden und der &Üuml;berschaubarkeit. Es ist auch noch nicht alles so eingefahren und festgefahren.
Meist ist bei meinen Aufgaben die polar-kartesische Koppelung inbegriffen. Manches ist hier nicht als Aufgabe ausformuliert, sondern als Anregung für Lehrende und Studierende, eigene Schritte in Facharbeiten etc.
|
www.mathematik-verstehen.de |
[Kurven]
[Analysis]
[Polarkoordinaten]
[Polar-Kartesisch
[Computer]
Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn |
Link zum Buch |
| www.leuphana.de/matheomnibus www.doerte-haftendorn.de https://mathe.web.leuphana.de http://www.mathematik-sehen-und-verstehen.de |